Пусть А1,А2,А3,А4,А5,А6– произвольный шестиугольник, и В1,В2,В3,В4,В5,В6– середины его сторон в порядке их следования. Докажите, что точки пересечения медиан треугольников В1В3В5 и В2В4В6 совпадают.

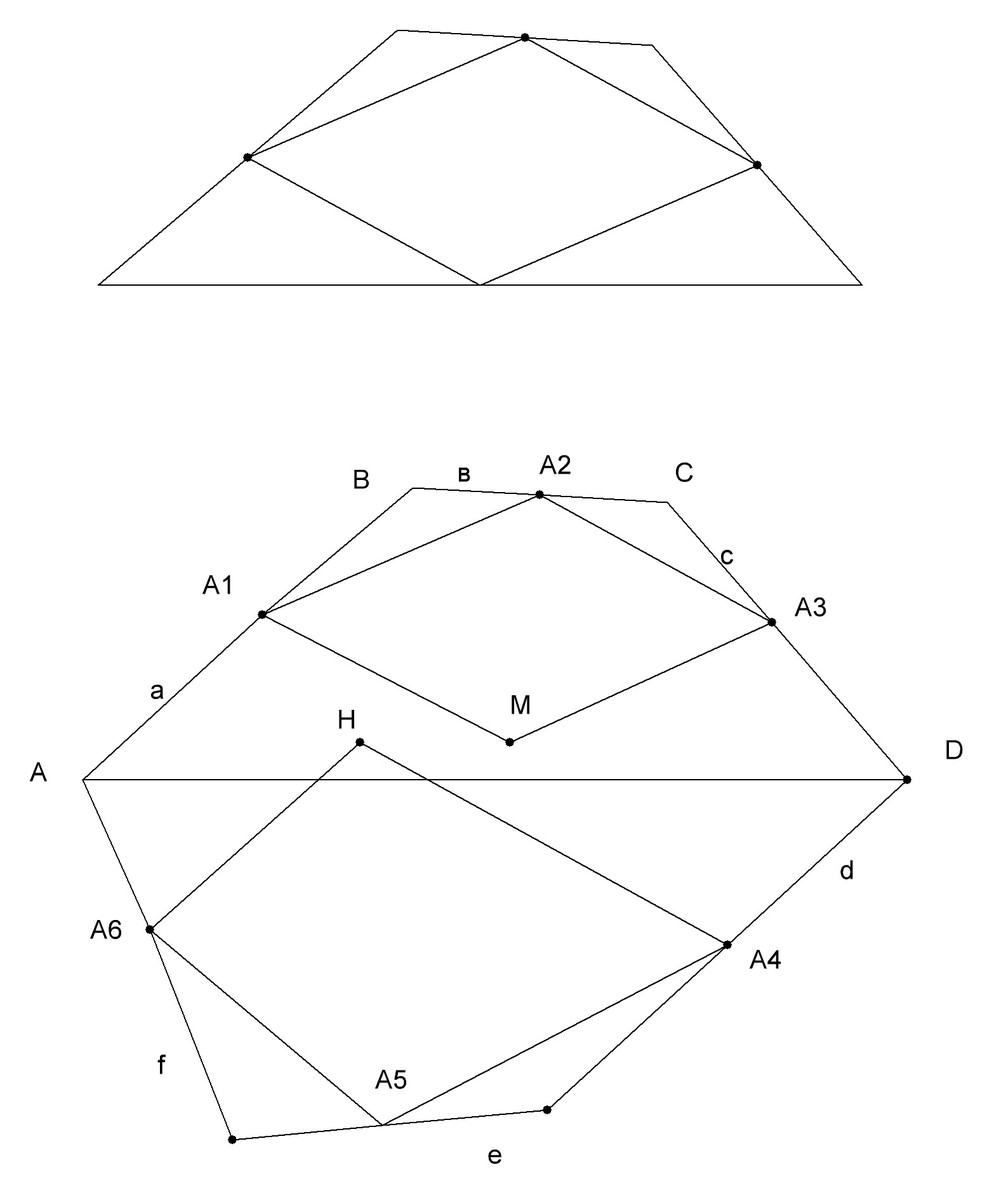
сначала начал рисовать в размер, потом умышленно нарисовал кривые "паралелограммы"

****с этой строки все записи - в векторном виде****

AA1=a; BA2=b; СA3=c; DA4=d; ....

AD=2a+2b+2c

A2A3=b+c

A1M=A2A3 - так как A1A2A3M - паралелограм

A1M=A2A3=b+c

AM=AA1+A1M=а+в+с = AD/2 - точка М лежит точно посредине АD

точно также доказывается что точка Н лежит точно посредине AD

значит М и Н - совпадают