-
tg в квадрате альфа - sin в квадрате альфа =sin в квадрате альфа умножить на tg в квадрате альфа
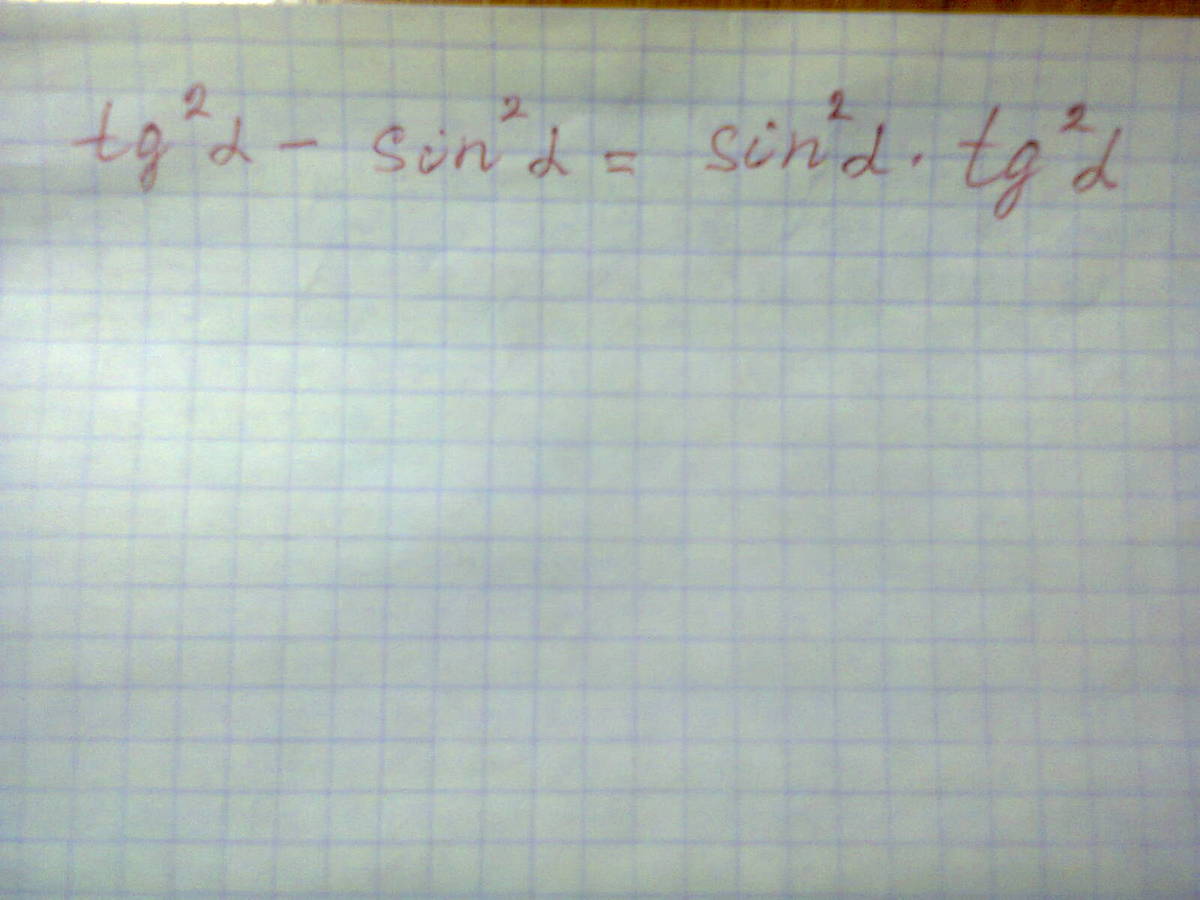
-
Предмет:
Математика -
Автор:
elliemccarthy - 6 лет назад
-
Ответы 1
-
-
Автор:
price - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какие главные строки из рассказа великан на поляне
-
Предмет:
Обществознание -
Автор:
kirad0fo - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
1*2+2*3+3*4+...+99*100 верно ли равенство
-
Предмет:
Математика -
Автор:
fatty - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Тесто для вареников содержит 16 частей творога, 2 части муки, 1 часть масла, 3 части сметаны и 3 части сахара. Найдите массу каждого продукта, необходимого для приготовления 1 кг теста?
-
Предмет:
Математика -
Автор:
chandlerzewa - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Степа сообщил о задуманном числе следущее: число делится на 5;число делится на 9;число делится 15.Сколько существует двузначных чисел,для которых два из этих утверждений истины а ложно
-
Предмет:
Математика -
Автор:
kellyvwkt - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
