Задать вопрос Регистрация
Помочь другим

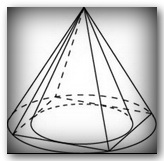
  • Во сколько раз объём конуса, описанного около правильной четырёхугольной пирамиды, больше объёма конуса, вписанного в эту пирамиду?

    question img

Ответы 1

  • Объём конуса равен трети произведения площади окружности-основания на высоту.V=\frac13SH=\frac13\pi RHРадиус основания описанного конуса равен \frac{\sqrt2}2t, где t - сторона основания пирамиды (сторона квадрата).Радиус основания вписанного конуса равен \frac12t.Тогда\frac{V_1}{V_2}=\frac{\frac13\pi\frac{\sqrt2}2t H}{\frac13\pi\frac12tH}=\sqrt2Объём описанного конуса больше объёма вписанного в \sqrt2 раз.

    • Автор:

      gromit
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years