-
Помогите пожалуйста найти
область сходимости функционального ряда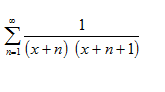
-
Предмет:
Математика -
Автор:
jeramiah - 6 лет назад
-
Ответы 1
-
Если в одном из слагаемых знаменатель обратится в ноль, то будем считать, что ряд расходится (т.к. в нём есть бесконечное слагаемое). В противном случае ряд сходится по признаку сравнения со сходящимся рядом 1/n^2.Ответ 1. Ряд сходится при всех x, кроме целых отрицательных.Замечание о "будем считать". Тут некоторая проблема в том, что слагаемые можно переписать в виде
Тогда частичная сумма равна (если все дроби конечны)
(Такой ряд часто называют "телескопическим", т.к. при раскрытии скобок почти все слагаемые сокращаются)Последнее слагаемое стремится к нулю (примерно как 1/N), так что сумма ряда равна
и очень хочется сказать, что ряд сходится при всех x, кроме -1 (а быть может возникающая бесконечность "сокращается" с такой же бесконечностью). Если понимать сумму ряда в таком смысле, то область сходимости станет более широкой.
-
Автор:
oliviamiller - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как сделать презентацию на тему : Индия
-
Предмет:
Другие предметы -
Автор:
mollie59pf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите неравенство 3+log
2x≥0
А
[1
8
;+∞)
Б
(0;1
8
]
В
(−∞;1
8
]
Г
[8;+∞)
Д
[−6;+∞)-
Предмет:
Математика -
Автор:
catwomanndud - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Один из корней уравнения 3х²+5х+2m=0 равен -1. Найдите второй корень
-
Предмет:
Математика -
Автор:
jocelynnwolf393 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В параллелограмме ABCD точка М-середина стороны АВ. Известно,что МС=МD. Докажите,что данный параллелограм-прямоугольникю
How much to ban the user?
1 hour
1 day
100 years
