Задать вопрос Регистрация
Помочь другим

  • ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ ПРИМЕР ПО МАТЕМАТИКЕ
    тема числовые ряды. признаки сходимости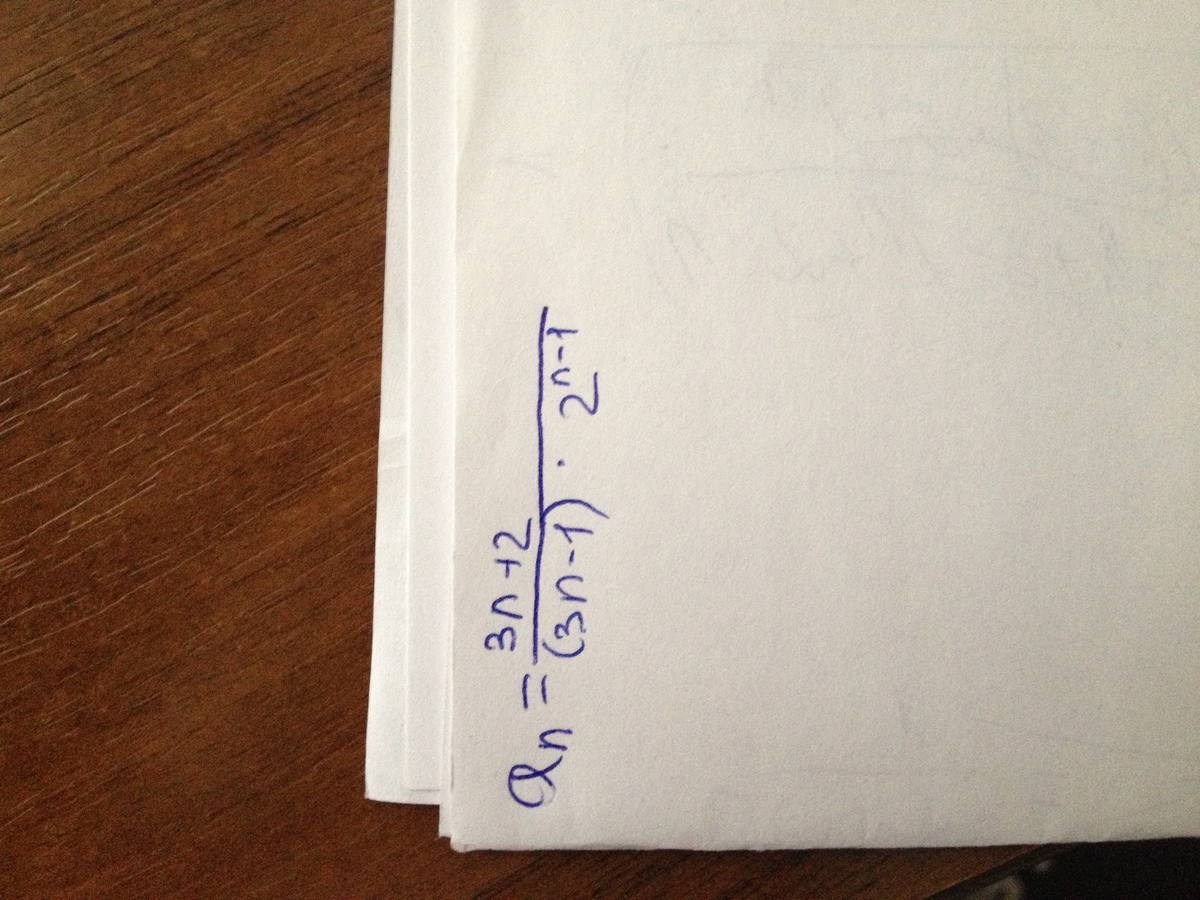

    question img

Ответы 1

  • Первым делом проверяем условие \forall n\in\mathbb{N} \ a_n \geq 0Смысл проверки в том, что для рядов с непостоянным знаком у нас есть только признак Вейерштрасса и признак Абеля, а значит - отпадают признаки неравенства, Даламбера,радикала, интеграла, |\sum_{n=0}^{\infty} a_n|<\infty \Leftrightarrow \ |\sum_{n=0}^{\infty} 2^na_{2^n}|<\infty и т.д...В данном случае ряд знак не меняет. Применяем радикальный признак:\limsup_{n\to\infty} \sqrt[n]{a_n} В данном случае последовательность сходится, значит \liminf=\limsup=\limПолучаем: \limsup_{n\to\infty}\sqrt[n]{a_n}=\frac{1}{2}<1Следовательно - ряд сходится.Напоминаю радикальный признак:\limsup_{n\to\infty} \sqrt[n]{a_n}=q\\ if \ q<1 \Rightarrow |\sum a_n|<\infty \\ if \ q>1 \Rightarrow |\sum a_n|=\infty \\ if q=1 \Rightarrow ?Ещё один способ - признак Даламбера. Он облегчает подсчёт предела последовательности, но если \liminf a_n<0 \ \land \ \limsup a_n>0 - ответа не даст. Потому применяется, в основном, если у последовательности есть предел по Коши.Признак Даламбера:\lim_{n\to\infty}|\frac{a_{n+1}}{a_n}|=\frac{1}{2}Условия схождения у Даламбера такие-же, как у радикального признака, потому повторно писать не буду.Вроде всё, если что не ясно - пиши.P.S. Архи-важная вещь по признаку Даламбера:\liminf_{n\to\infty}\frac{a_{n+1}}{a_n}>1 \Rightarrow|\sum_{n=0}^\infty a_n|=\infty \\ \limsup_{n\to\infty}\frac{a_{n+1}}{a_n}<1 \Rightarrow|\sum_{n=0}^\infty a_n|<\infty \\ (\limsup_{n\to\infty}\frac{a_{n+1}}{a_n}>1 \ or \ \liminf_{n\to\infty}\frac{a_{n+1}}{a_n}<1 \ means \ nothing\\ \\

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years