Задать вопрос Регистрация
Помочь другим

  • Решите уравнение

    log4(25^(x+3) - 1) = 1 + log4(5^(x+3) + 1)

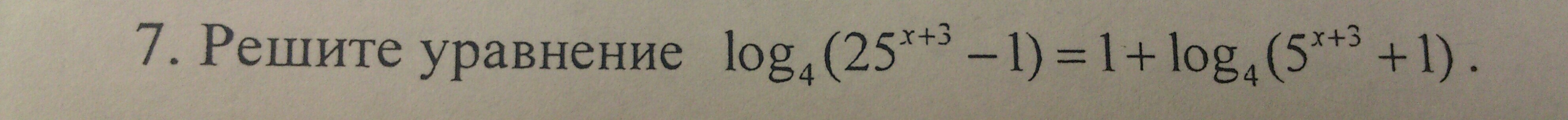
    question img

Ответы 1

  • Представим 1 как log_4 (4)

    log4(25^(x+3) - 1 = log_4 (4) + log4(5^(x+3) + 1)

    Согласно свойству логарифмов, при сложении логарифмов с одинаковым основанием их показатели умножаются.

    log4(25^(x+3) - 1) = log4((5^(x+3) +1)4)

    Основания одинаковые, теперь мы можем пропотенциировать наше уравнение. Одновременно я представлю 25^x+3 как 5^2(x+3)

    5^2(x+3) - 1 = 5^(x+3) *4 + 4

    Введем замену:

    5^(x+3) = a

    a^2 - 1 = 4a + 4

    Перенесем все в левую часть

    a^2 - 4a - 5 = 0

    По теореме виета находим корни:

    x1 = 5; x2 = -1

    Возвращаемся к замене. Второй корень нам не подходит, посему работаем с первым.

    5^x+3 = 5^1

    Основания одинаковые, мы можем их откинуть.

    x + 3 = 1

    x = -2

    Ответ: x = -2

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years