-
Исследуйте функцию y=e^4x (2-3x) на монотонность и экстремумы.
11 класс, решение без экспоненты нужно.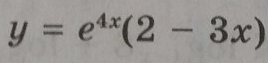
Ответы 1
-
Решениеy = (e^(4*x))*(2-3*x)1. Находим интервалы возрастания и убывания. Первая производная.f'(x) = 4 * (-3x+2) * e^(4x) - 3 * e^(4x)илиf'(x) = (-12x+5) * e^(4x)Находим нули функции. Для этого приравниваем производную к нулю(-12x+5) * e^(4x) = 0Откуда:- 12x + 5 = 0- 12x = - 5x₁ = 5/12(-∞ ;5/12) f'(x) > 0 функция возрастает(5/12; +∞) f'(x) < 0 функция убываетВ окрестности точки x = 5/12 производная функции меняет знак с (+) на (-). Следовательно, точка x = 5/12 - точка максимума.2) Hаходим первую производную функции:f'(x) = 4*(-3x+2) * e^(4x) - 3 * e^(4x)илиf'(x) = (-12x+5) * e^(4x)Находим нули функции. Для этого приравниваем производную к нулю(-12x+5) * e^(4x) = 0- 12x + 5 = 0- 12x = - 5Откуда:x₁ = 5/12Вычисляем значения функции f(5/12) = (3*(e⁵/³))/4Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:y'' = 16*(- 3x + 2) * e^(4x) - 24 * e^(4x)илиy'' = (- 48x + 8) * e^(4x)Вычисляем:y``(5/12) = ((- 48 *(5/12) + 8) * e^(4*(5/12)) = - 12 * e⁵/³ = < 0Следовательно, в этой точке функция имеет максимум:y(5/12) = e^(4*(5/12)) * (2-3*(5/12)) = e⁵/³ * (2 - 5/4) = (3*(e⁵/³))/4ymax (5/12) = (3*(e⁵/³))/4
-
Автор:
george92 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
№ 330
Для руско-язичних: За даными таблицы найди,сколько ткани использовали для пошивки одной наволочки.
Наволочка
Простынь
-
Предмет:
Математика -
Автор:
winniegndg - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
спиши.вставляя пропущеные буквы площади площа...ь.грузы гру... соседи сосе
-
Предмет:
Русский язык -
Автор:
alanawarren - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Определите число молей воздуха в комнате объемом 5*6*3 м при температуре 27 градусов и давлении 10 Па
-
катер против течении реки прошел 96 км в пути за 8 часов. за сколько часов пройдет катер тот же путь в обратном направлении если скорость тесения реки 2 км / ч
-
Предмет:
Математика -
Автор:
aubreeholland - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
