-
Исходя из определения предела последовательности докажите, что при n стрелочка бесконечность.
Пример на фото.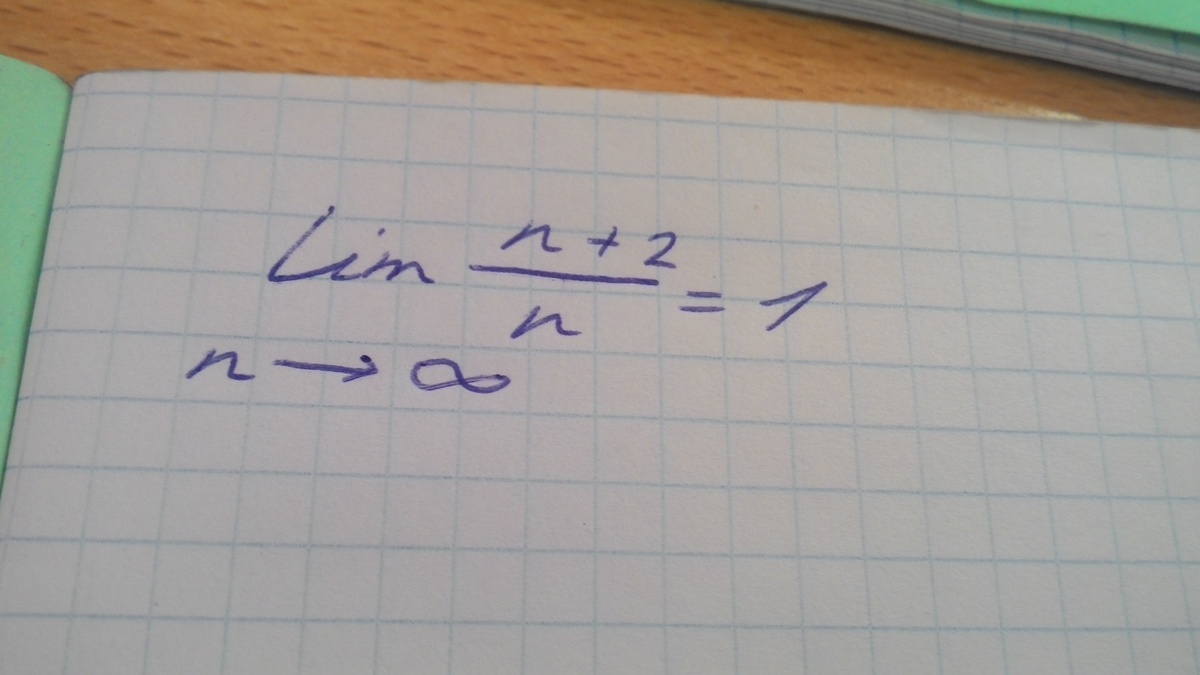
-
Предмет:
Алгебра -
Автор:
jayden7ulv - 6 лет назад
-
Ответы 1
-
Следуя определению предела последовательности:\displaystyle a= \lim _{n\rightarrow +\infty} x_nЕсли:\forall \epsilon , \exists N \in \mathbb N | \forall n \ \textgreater \ N \Rightarrow |x_n-a|\ \textgreater \ \epsilonНа понятном языке это так: Число называется пределом последовательности, если для любой его окрестности \forall \epsilon существует натуральный номер \exists N\in \mathbb N - такой, что все члены последовательности с большими номерами \forall n \ \textgreater \ N окажутся внутри окрестности |x_n-a| \ \textgreater \ \epsilonИмеем предел:\displaystyle \lim_{n \to \infty} \frac{n+2}{n} =1Требуется доказать что он равен 1. Доказательство:Если n\ \textgreater \ N то |\frac{n+2}{n} -1|\ \textless \ \epsilon \Rightarrow | \frac{n-n+2}{n} |\ \textless \ \epsilon \Rightarrow | \frac{2}{n} | \ \textless \ \epsilonТак как само n натурально, то мы имеем право раскрыть данный модуль:\frac{2}{n} \ \textless \ \epsilon \Rightarrow n\ \textgreater \ \frac{2}{\epsilon} Следовательно, отсюда имеем следующее:Если n \ \textgreater \ N то n \ \textgreater \ \frac{2}{\epsilon}Так как в:n \ \textgreater \ \frac{2}{\epsilon} дробное число, нам следует брать только его целую часть:n\ \textgreater \ [\frac{2}{\epsilon}]Имеем:N=[ \frac{2}{\epsilon}] Вывод:Для любой сколько угодно малой окрестности \epsilon точки a=1, нашлось значение N=[ \frac{2}{\epsilon}] , такое , что для любых больших номеров n\ \textgreater \ N выполняется неравенство | \frac{n+2}{n} -1|\ \textless \ \epsilonТаким образом, число a является пределом последовательности по определению. Ч.Т.Д.
-
Автор:
barrettmndg - 2 года назад
-
7
-
-
Добавить свой ответ
Еще вопросы
-
Решите уравнение с объяснениями пожалуйста x^3-6x+4=0
-
Предмет:
Алгебра -
Автор:
lilianwxjl - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Запишите одно-два предложения используя данные слова петушок курочка зёрнышко подавился
-
Предмет:
Русский язык -
Автор:
jayvon - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
2/15*21/22 умножение не помню
-
Предмет:
Математика -
Автор:
maggie-moocamacho - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
запиши какие числа пропущены в выражении А9+2А=Б4
-
Предмет:
Математика -
Автор:
mollie59pf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
