-
СРОЧНО!!!! прошу срочно решить. Помогите пожалуйста, буду очень благодарен!)
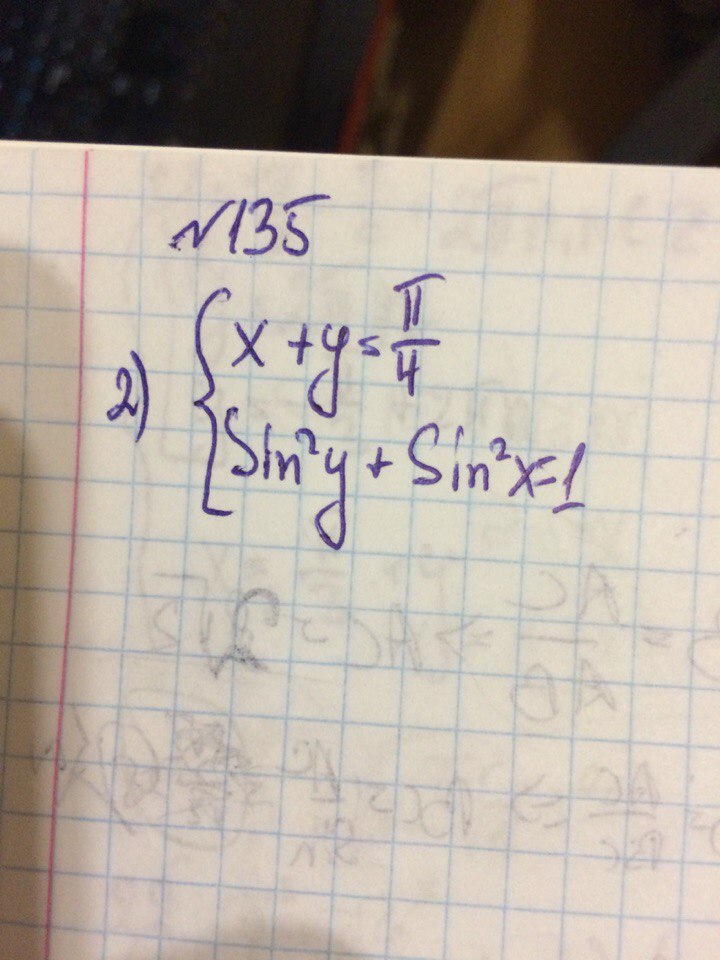
Ответы 4
-
Доброй ночи, простите, что с "черного входа", иначе пока не умею, я отметила нарушение (спам), а все осталось на месте,
-
Автор:
maldonado - 6 лет назад
-
0
-
-
№17752824
-
Автор:
connornguyen - 6 лет назад
-
0
-
-
здраствуйте, да. человек задал вопрос в ответе, хотя мог просто отправить комментарий под заданием
-
Автор:
valentín35 - 6 лет назад
-
0
-
-
| :
∈
∈
∈
∈
∈
Ответ:
∈
-
Автор:
caratfwt - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Прочитайте предложения, перепишите их, вставляя в пропуски
определённый или неопределённый артикль там, где необходимо:
1. The Lloyds Bank Review is published four times ___ year.
2. ___ Computer software is not as expensive as you may think.
3. Where is ___ file I gave you this morning?
4. ___ Money is ___ root of all evil.
5. ___ rich do not do enough to help ___ poor.
6. CD-ROMs can store large quantities of ___ information.
7. Should the government do more to help ___ unemployed?-
Предмет:
Английский язык -
Автор:
fun size - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
найдите сумму всех натуральных чисел кратных 7 и не превосходящих 133
-
Предмет:
Алгебра -
Автор:
camilledzqz - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
поставьте данные существительные в родительный падеж множественного числа
КРОССОВКИ, АНГЛИЧАНЕ, КАДЕТ, ГРАММ, АМПЕР, ШОРТЫ, МОНГОЛЫ САПЕРЫ-
Предмет:
Русский язык -
Автор:
pedrowpxb - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Тригонометрия
Найти tg(П/2+x)+ctg(П-х),где Sinx=-0.6 (4 четверть)-
Предмет:
Алгебра -
Автор:
cassidy8nkn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
