Задать вопрос Регистрация
Помочь другим

  • СРОЧНО!! 100 БАЛЛОВ!! Надо дорешать задачу! Вычислите площадь фигуры ограниченной линиями [tex]y= 3^{x} [/tex], [tex]y= 9^{x} [/tex], [tex]x=1[/tex]. Надо ещё начертить график!

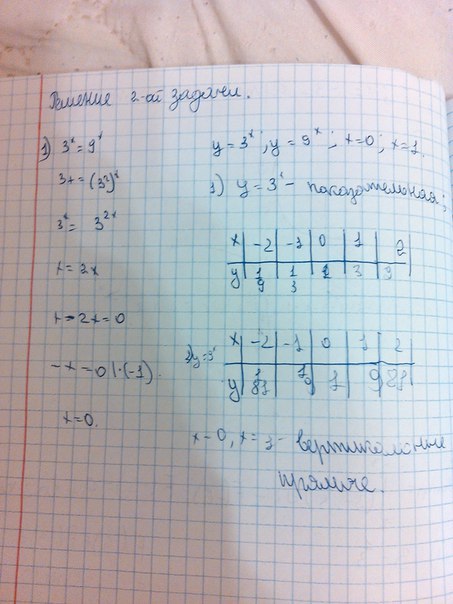
    question img

Ответы 2

  • Находим точки пересечения графиков:3ˣ=9ˣ3ˣ=3²ˣх=2хх=0Поулчаем пределы интегрированиях=0, второе значение х=1 - даноS= \int\limits^1_0 {(9^x-3^x)} \, dx =(\frac{9^x}{ln9}- \frac{3^x}{ln3})^1_0= (\frac{9^1}{ln9}- \frac{3^1}{ln3})-(\frac{9^0}{ln9}- \frac{3^0}{ln3}) = \\ \\ =(\frac{9}{ln9}- \frac{3}{ln3})-(\frac{1}{ln9}- \frac{1}{ln3}) = \\ \\=\frac{8}{ln3^2}- \frac{2}{ln3}=\frac{8}{2ln3}- \frac{2}{ln3} =\frac{4}{ln3}- \frac{2}{ln3} = \frac{2}{ln3}
  • Найдем отрезок на котором определенна фигура.Для этого сравним 2 функции.3^x=9^x3^x=3^{2x}x=2xx=0Последняя граница нам уже дана.Поэтому имеем отрезок:[0,1]Отсюда определенный интеграл: \int\limits^1_0 {9^x-3^x} \, dx= \frac{9^x}{\ln 9}- \frac{3^x}{\ln 3}\Big|_0^1=\frac{9}{\ln 9}- \frac{3}{\ln 3}-\frac{1}{\ln 9}+\frac{1}{\ln 3}= \frac{8}{2\ln 3}- \frac{3}{\ln 3}+\frac{1}{\ln 3}= \frac{4-3+1}{\ln3}= \frac{2}{\ln3} График во вложении.P.S.Красный график 9^x
    answer img

    • Автор:

      zoe
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years