Задать вопрос Регистрация
Помочь другим

  • Вычислить предел( любой , желательно первый) . Решите пожалуйста , не могу решить, а скоро экзамен... ( задание в приложении

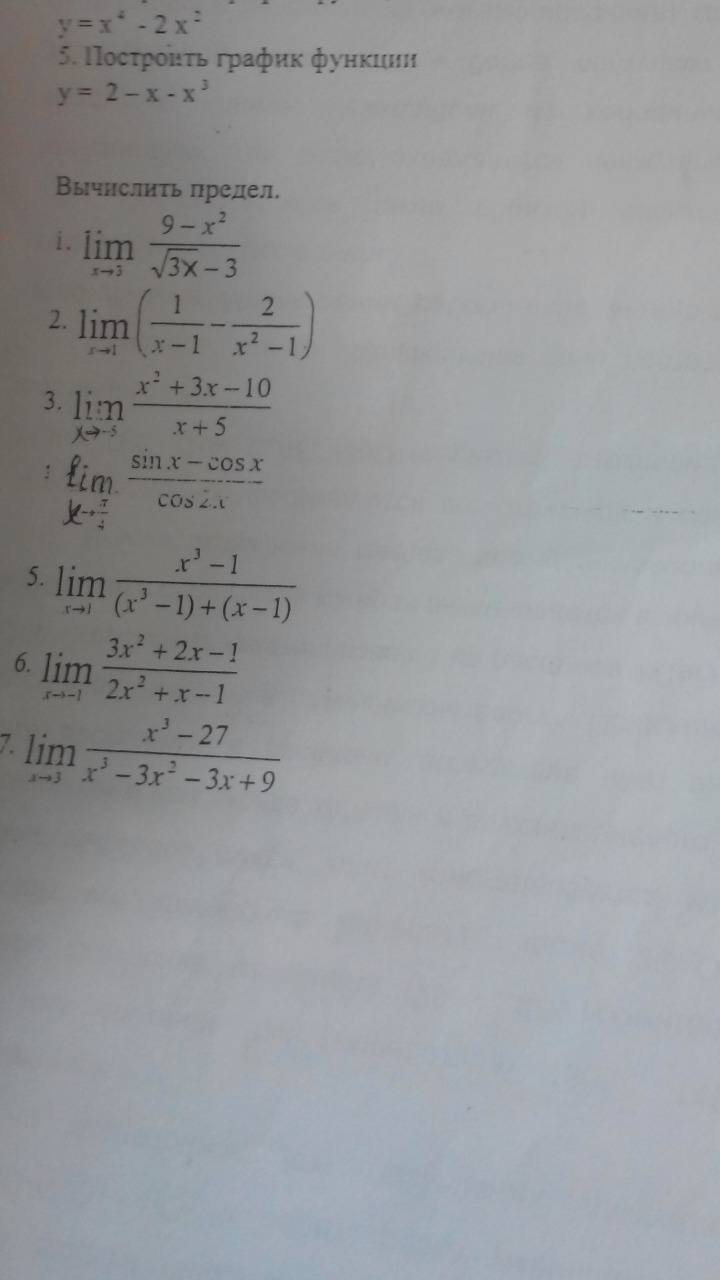
    question img

Ответы 1

  • 1. \lim_{x \to \3} \frac{9-x^2}{ \sqrt{3x}-3 }= \lim_{x\to \3} (- \frac{(x-3)(x+3)}{ \sqrt{3x}-3 } )= \\ =lim_{x \to \3} (- \frac{( \sqrt{x} - \sqrt{3} )( \sqrt{x} + \sqrt{3} )(x+3)}{ \sqrt{3}( \sqrt{x} - \sqrt{3} ) } ) = \\ \\ = \lim_{x \to \3} (- \frac{( \sqrt{x} + \sqrt{3} )(x+3)}{ \sqrt{3}} )=- \frac{( \sqrt{3}+ \sqrt{3} )(3+3)}{ \sqrt{3} }= \\ \\ =- \frac{2 \sqrt{3}*6 }{ \sqrt{3} }=-12 2. \lim_{x \to \1} ( \frac{1}{x-1}- \frac{2}{x^2-1} )= \lim_{x \to \1} ( \frac{1}{x-1}- \frac{2}{(x-1)(x+1)} )= \\ \\ = \lim_{x \to \1} ( \frac{x+1-2}{(x-1)(x+1)} )= \lim_{x \to \1} \frac{x-1}{(x-1)(x+1)}= \\ \\ = \lim_{x \to \1} \frac{1}{x+1}= \frac{1}{1+1}= \frac{1}{2}=0.5 3.Разложим x²+3x-10 на множители:x²+3x-10=0D=9+40=49x₁=(-3-7)/2= -5x₂=(-3+7)/2=2x²+3x-10=(x+5)(x-2) \lim_{x \to \--5} \frac{x^2+3x-10}{x+5}= \lim_{x \to \--5} \frac{(x+5)(x-2)}{x+5}= \\ \\ = \lim_{x \to \--5} (x-2)=-5-2=-7 4. \lim_{x \to \- \frac{ \pi }{4} } \frac{sinx-cosx}{cos2x}= \lim_{x \to \ \frac{ \pi }{4} } (- \frac{cosx-sinx}{cos^2x-sin^2x} )= \\ \\ = \lim_{x \to \ \frac{ \pi }{4} } (- \frac{cosx-sinx}{(cosx-sinx)(cosx+sinx)} )= \lim_{x \to \ \frac{ \pi }{4} } (- \frac{1}{cosx+sinx} )= \\ \\ =- \frac{1}{cos \frac{ \pi }{4}+sin \frac{ \pi }{4} }=- \frac{1}{ \frac{ \sqrt{2} }{2}+ \frac{ \sqrt{2} }{2} }= - \frac{1}{ \sqrt{2} }= - \frac{ \sqrt{2} }{2} 5. \lim_{x \to \ 1} \frac{x^3-1}{(x^3-1)+(x-1)}= \lim_{x \to \ 1} \frac{(x-1)(x^2+x+1)}{(x-1)(x^2+x+1)+(x-1)}= \\ \\ = \lim_{x\to \ 1} \frac{(x-1)(x^2+x+1)}{(x-1)(x^2+x+1+1)}= \lim_{x \to \ 1} \frac{x^2+x+1}{x^2+x+2}= \\ \\ = \frac{1^2+1+1}{1^2+1+2}= \frac{3}{4}=0.75 6.Разложим на множители:3x²+2x-1=0D=4+12=16x₁=(-2-4)/6=-1x₂=(-2+4)/6=2/6=1/33x²+2x-1=3(x+1)(x - ¹/₃) = (x+1)(3x-1)Разложим на множители:2x²+x-1=0D=1+8=9x₁=(-1-3)/4=-1x₂=(-1+3)/4=2/4=1/22x²+x-1=2(x+1)(x-¹/₂)=(x+1)(2x-1) \lim_{x \to \ -1} \frac{3x^2+2x-1}{2x^2+x-1} = \lim_{x \to \ -1} \frac{(x+1)(3x-1)}{(x+1)(2x-1)}= \\ \\ = \lim_{x \to \ -1} \frac{3x-1}{2x-1}= \frac{3*(-1)-1}{2*(-1)-1}= \frac{-4}{-3}=4/3=1 \frac{1}{3} 7. \lim_{x \to \ 3} \frac{x^3-27}{x^3-3x^2-3x+9} = \lim_{x \to \ 3} \frac{(x-3)(x^2+3x+9)}{x^2(x-3)-3(x-3)}= \\ \\ = \lim_{x \to \ 3} \frac{(x-3)(x^2+3x+9)}{(x-3)(x^2-3)}= \lim_{x \to \ 3} \frac{x^2+3x+9}{x^2-3}= \\ \\ = \frac{3^2+3*3+9}{3^2-3}= \frac{9+9+9}{9-3}= \frac{27}{6}= \frac{9}{2}=4.5

    • Автор:

      tysonhfdj
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years