-
Как решать подобные иррациональные неравенства? Нужно объяснение.
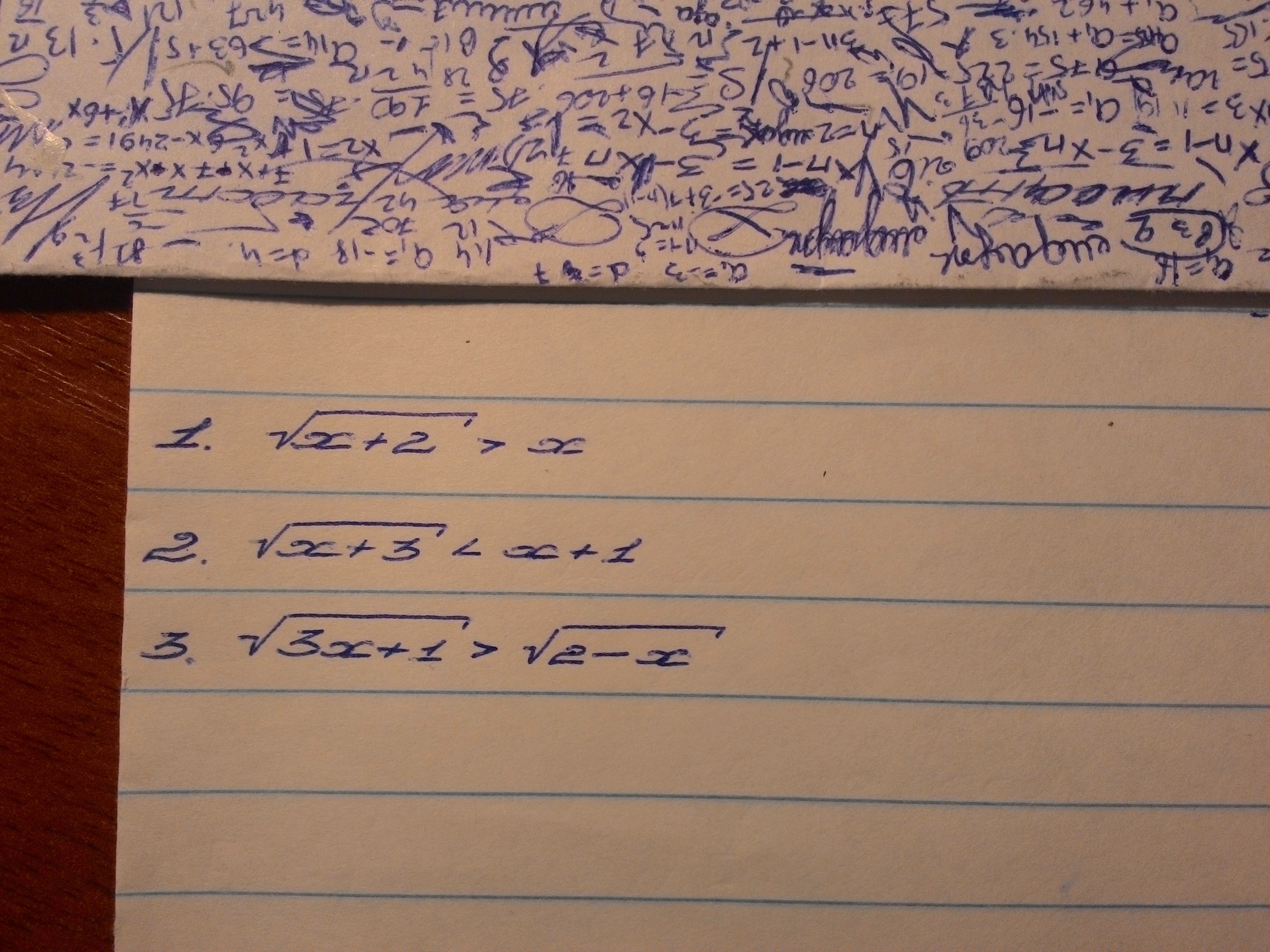
-
Предмет:
Алгебра -
Автор:
kristinamcbride - 6 лет назад
-
Ответы 1
-
Ну, это просто.1. √(x+2)>xРассматриваем два случая. Если x<0, то, так как корень больше любого отрицательного числа,x должен просто принадлежать одз корня. Получаем систему:{x+2≥0{x<0-2≤x<0 - это часть ответа. Теперь пусть x≥0. Тогда обе части неотрицательны, а значит мы имеем право возвести неравенство в квадрат. Система:{x+2>x²{x≥0Получаем 0≤x<2А теперь объединяем полученные решения и пишем ответ: -2≤x<22. √(x+3)<x+1Начинаем рассуждать. Если левая часть меньше нуля, то есть если x<-1, неравенство решений не имеет, ведь корень всегда больше или равен нулю. Значит первое условием x≥-1. Причем в таком случае и с одз корня (x≥-3) все в порядке. Теперь, раз обе части неотрицательны возводим в квадрат, не забывая об условии записанном выше:{x+3<(x+1)²{x≥-1Ответ: x>1Ну и последнее:√(3+2x)>√(2-x)Здесь достаточно найти одз правого корня x≤2 и корни сразу же отбросить{3+2x>2-x{x≤2Это переход равносилен потому что если 2-x≥0, то раз 3+2x>2-x, то 3+2x уж подавно больше ноля. А значит и одз левого корня учтено.Ответ: -1/3<x≤2
-
Автор:
kayden96 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Окружность, радиус которой равен 36, вписана в равнобедренную трапецию. Она
касается боковой стороны в точке, которая делит эту сторону в отношении 3 : 4.
Найдите периметр трапеции.-
Предмет:
Математика -
Автор:
martínezodyo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Атомный номер вещества, которое способны фиксировать бактерии Rhizobium.
-
В правильной треугольной пирамиде SABC через сторону АС основания проведено
сечение АСМ под углом 60° к плоскости основания АВС. Точка М делит ребро SВ так,
что SМ : МВ = 1 : 3. Найдите объем пирамиды МABC, если AВ = 34.-
Предмет:
Математика -
Автор:
forbes - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ПОМОГИТЕ ОЧЕНЬ НАДО!!! И ПО БЫСТРЕЕ!!! :((
Спиши слова, разделяя их для переноса. Подчеркни одной чертой слова, в которых звуков больше, чем букв. Подчеркни двумя чертами слова, в которых, букв больше, чем звуков.
Школьный, двойка, дочь, соловей, Юля, прыгать, дорогая, урок, группа.
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
-
Предмет:
Русский язык -
Автор:
zoeyxpdm - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
