-
Логарифмическое неравенство
Заранее огромное спасибо!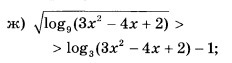
-
Предмет:
Алгебра -
Автор:
arcadioy6uv - 6 лет назад
-
Ответы 2
-
Спасибо Вам большое!!!
-
Автор:
parker2 - 6 лет назад
-
0
-
-
Сразу напрашивается замена
. Тогда
Если t<1 неравенство выполняется при любом t≥0. Значит часть решения выглядит так: 0≤t<1Если t≥1 мы имеем право возвести обе части в квадрат:
Объединим оба полученных промежутка и получим 0≤t<2. Возвращаемся к замене:
Решаем и получаем ответ: (-1; 1/3] U [1; 7/3)
-
Автор:
cubbyaiuc - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
2,38/(2x-4,42)=2 9/50(дробь)
-
Предмет:
Математика -
Автор:
allieemml - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Give him his letters if he turns …. 2. I turned … and saw Mary’s face in a window. 3. “I’ll turn you … a frog!” said the Witch to the Prince. 4. He turned the whole house … trying to find some up-to-date information on computers. 5. He couldn’t sleep but just turned … in his bed till 6 o’clock in the morning. 6. Charles turned … to be a very good friend; he was really very helpful when I was in trouble. 7. The wind was so strong that it turned out umbrellas … … . 8 Will you turn the television … : I have a problem hearing what mother is saying. 9. In a few seconds six white mice turned … six beautiful horses. 10. Elizabeth was turning … the pages of her book without reading.
-
Предмет:
Английский язык -
Автор:
katieharrison - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
[tex]3 ^{72} *( \frac{1}{3} ) ^{x} *( \frac{1}{3} ) ^{ \sqrt{x} } \ \textgreater \ 1[/tex]
and
[tex]3*4^{x} +2*9 ^{x} -5*6 ^{x} \ \textless \ 0[/tex] -
Синквейн к стихотворению оттепель Николай Заболоцкий вот стих пожалуйста напишите дам 25 баллов Оттепель после метели.
Только утихла пурга,
Разом сугробы осели
И потемнели снега.
В клочьях разорванной тучи
Блещет осколок луны.
Сосен тяжелые сучья
Мокрого снега полны.
Падают, плавятся, льются
Льдинки, втыкаясь в сугроб.
Лужи, как тонкие блюдца,
Светятся около троп.
Пусть молчаливой дремотой
Белые дышат поля,
Неизмеримой работой
Занята снова земля.
Скоро проснутся деревья,
Скоро, построившись в ряд,
Птиц перелетных кочевья
В трубы весны затрубят.
-
Предмет:
Литература -
Автор:
anastasia83 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
