Решите. пожалуйста, 100баллов, срочно прошшшууууууу. завтра нужно уже сдать

Решите. пожалуйста, 100баллов, срочно прошшшууууууу. завтра нужно уже сдать
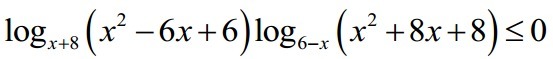
- Предмет:
  Алгебра
- Автор:
  gabrielksse
- 6 лет назад

Ответы 4

х=3 не входит в область определения. поэтому вы не можете выбирать такое число
- Автор:
  slinkykboy
- 6 лет назад
- 0
в ответе есть оно ?
- Автор:
  veronica33
- 6 лет назад
- 0
если промижуток (3-sqrt(3), 3+sqrt(3)) то 3 входит в промижуток ..... значит ответ неверен .... Я писал что надо ответ исправить
- Автор:
  leo4
- 6 лет назад
- 0
Решить неравенство: $\log_{x+8}(x^2-6x+6)\log_{6-x}(x^2+8x+8) \leq0$ Рассмотрим функцию: $f(x)=\log_{x+8}(x^2-6x+6)\log_{6-x}(x^2+8x+8)$ Область определения функции: $\begin{cases} & \text{ } x^2-6x+6\ \textgreater \ 0 \\ & \text{ } x^2+8x+8\ \textgreater \ 0 \\ & \text{ } x+8\ \textgreater \ 0 \\ & \text{ } 6-x\ \textgreater \ 0 \\ & \text{ } x+8e 1 \\ & \text{ } 6-xe 1 \end{cases}$ $\begin{cases} & \text{ } x^2-6x+6\ \textgreater \ 0 \\ & \text{ } x^2+8x+8\ \textgreater \ 0 \\ & \text{ } x\ \textgreater \ -8 \\ & \text{ } x\ \textless \ 6 \\ & \text{ } xe5 \\ & \text{ } xe-7 \end{cases}$ решим 1 и 2 неравенство из системы неравенств. $x^2-6x+6\ \textgreater \ 0$ Приравняем к нулю $x^2-6x+6=0\\ D=b^2-4ac=(-6)^2-4\cdot1\cdot6=36-24=12$ $D\ \textgreater \ 0$ , значит квадратное уравнение имеет 2 действительных корней, найдем их. $x_1_,_2= \dfrac{-b\pm \sqrt{D} }{2a}$ $x_1_,_2= \dfrac{6\pm \sqrt{12} }{2} = \dfrac{6\pm2 \sqrt{3} }{2} =3\pm \sqrt{3}$ __+__(3-√3)___-__(3+√3)__+___>Аналогично решим и другое неравенство. $x^2+8x+8\ \textgreater \ 0\\x^2+8x+8=0\\ D=b^2-4ac=64-32=32;\\ \\ x_3_,_4= \dfrac{-8\pm4 \sqrt{2} }{2} =-4\pm2 \sqrt{2}$ __+__(-4-2√2)_____-___(-4+2√2)____+____Запишем область определения функции: $D(f)=(-8;-7)\cup(-7;-4-2 \sqrt{2} )\cup(-4+2 \sqrt{2} ;3- \sqrt{3} )\cup\\ \\ \cup(3+ \sqrt{3} ;5)\cup(5;6)$ Приравниваем функцию к нулю. $f(x)=0;\,\,\,\log_{x+8}(x^2-6x+6)\log_{6-x}(x^2+8x+8)=0$ Произведение равно нулю, значит:1) $\log_{x+8}(x^2-6x+6)=0$ По свойству логарифмов: $\log_{x+8}(x^2-6x+6)=\log_{x+8}1\\ x^2-6x+6=1\\ x^2-6x+5=0$ По т. Виета: $x_1=1;\,\,\,\,x_2=5$ 2) $\log_{6-x}(x^2+8x+8)=0\\ \log_{6-x}(x^2+8x+8)=\log_{6-x}1\\ x^2+8x+8=1\\ x^2+8x+7=0$ По т. Виета: $x_1=-1;\,\,\, x_2=-7$ Решив с учетом ОДЗ, имеем вот такой ответ: $x \in (-8;-4-2 \sqrt{2} )\cup(2 \sqrt{2} -4;-1]\cup[1;3- \sqrt{3} )\cup(3+\sqrt{3} ;5)\cup(5;6).$
- Автор:
  burnett
- 6 лет назад
- 0
Добавить свой ответ