-
Пожалуйста, помогите решить 30.27! Естественно с объяснениями!
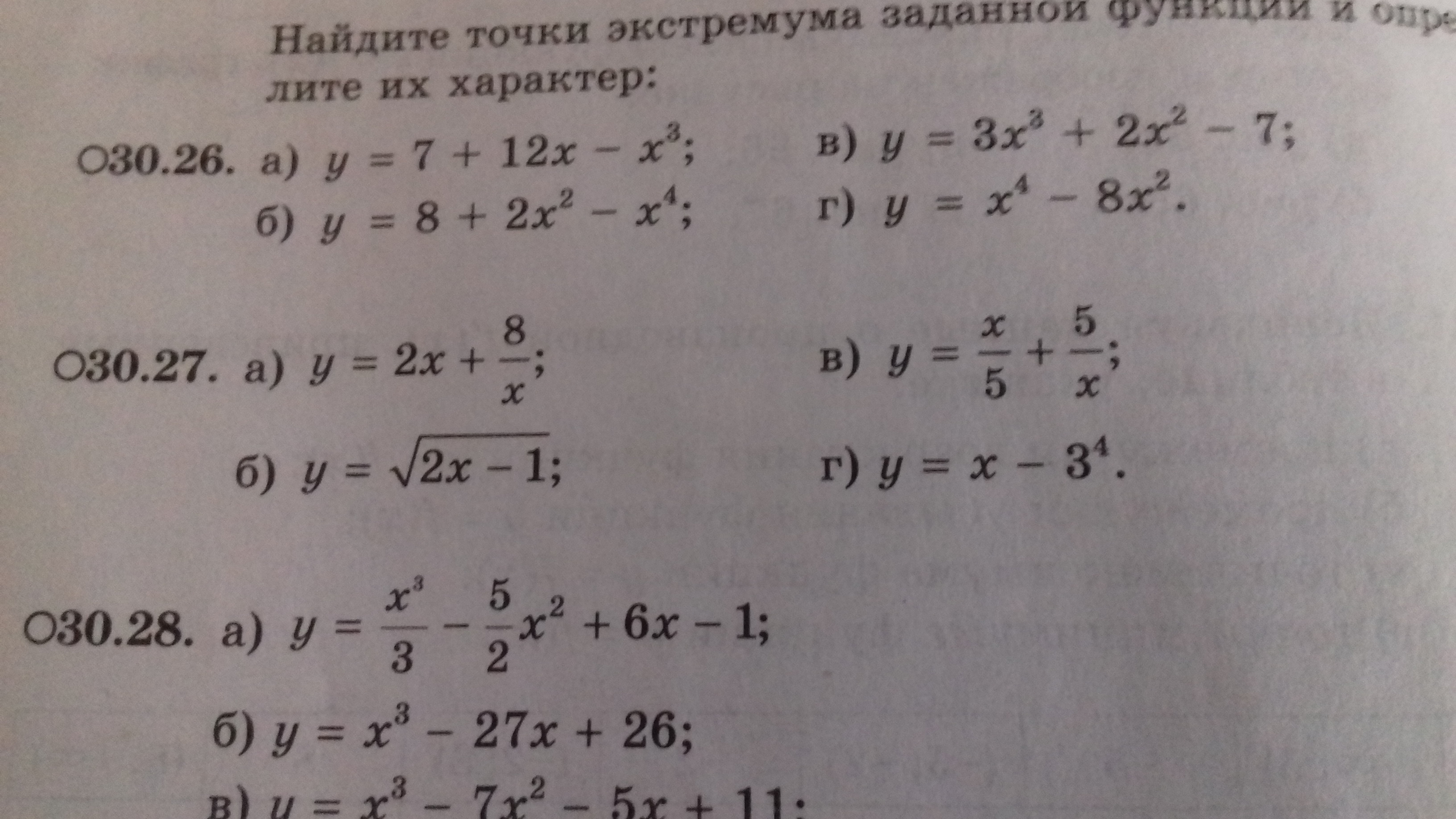
-
Предмет:
Алгебра -
Автор:
marleyweeks - 6 лет назад
-
Ответы 4
-
Почему здесь деление? (2x² -8)/x²
-
Автор:
roxyxdgy - 6 лет назад
-
0
-
-
2/1 - 8/x² = (2x² -8)/x² привёл к общему знаменателю.
-
Автор:
cheese49 - 6 лет назад
-
0
-
-
Спасибо
-
Автор:
ismael - 6 лет назад
-
0
-
-
а) у = 2х +8/хy' = 2 - 8/x² = (2x² -8)/x²(2x² -8)/x² = 02x² - 8 = 0, ⇒ x = +-2x²≠ 0, ⇒ x ≠ 0вывод: х = 0 - это точка разрыва. Проверим х =+-2-∞ -2 0 2 +∞ + - + знаки производнойх = -2 - это точка максимума х = 2 - это точка минимума х = 0 - это точка разрываб) у = √(2х -1)y' =1/√(2x -1)производная ≠ 0, значит, у данной функции нет точек экстремума, значит, нет точек максимума и нет точек минимума.х = 1/2 - это точка разрывав) у = х/5 +5/хy' = 1/5 - 5/х²= (х² -25)/5х²(х² -25)/5х²=0х² -15 = 0, ⇒ х = +-5 х ≠ 0- ∞ -5 0 5 +∞ + - - + это знаки производнойвывод: х = -5 - это точка максимума, х = 5 - это точка минимума;х = 0 - это точка разрываг) у = х - 3⁴y' = 1 > 0данная функция не имеет критических точек, данная функция монотонная (возрастающая).
-
Автор:
boomhauer - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите с уравнением!!! желательно с решением. Зарание спасибо 10*(1.37k-0.12k):5:8=0 плиииииииииииииз молюю
-
Предмет:
Математика -
Автор:
fresier - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
построить от ля D7 с его обращениями и разрешить в мажор и минор
-
Предмет:
Музыка -
Автор:
eulalianichols - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Одна сторона прямоугольника на 14 см меньше другой,а его площадь равна 240 см^2.Найдите стороны прямоугольника
-
Предмет:
Алгебра -
Автор:
esmeraldasims - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
нарисуй любимую еду . Затем напиши предложения. Chimps like............
-
Предмет:
Английский язык -
Автор:
jordan905 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
