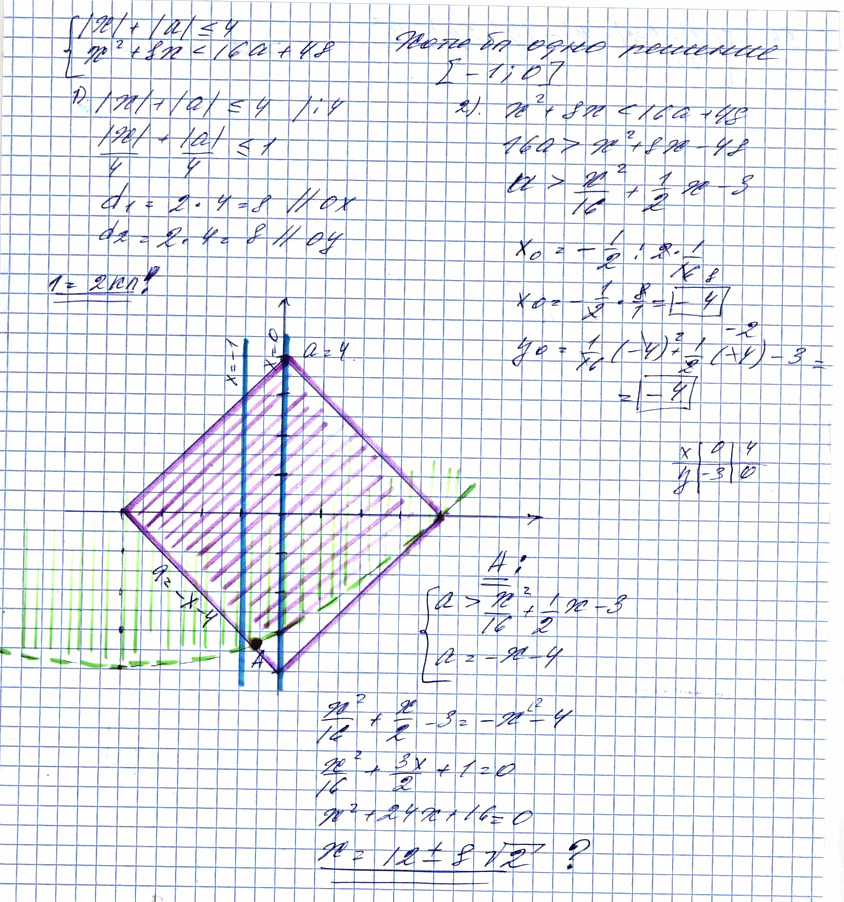
Помогите, пожалуйста, ДОРЕШАТЬ ЗАДАЧУ С ПАРАМЕТРОМ. Осталось найти координаты точки А, как это сделать?

У меня получилось 2 корня 12 +- 8√2. Какой из них относится к (.) А?

В ответе 8 - 8√2 < а ≤ 4

Вместо того, чтобы кто-то из модераторов решил задачу и указал мне на ошибки, мой ответ проверили и признали лучшим!

Из 1 неравенства|x| + |a| <= 4{ x ∈ [-4; 4]; a ∈ [-4; 4]Если x ∈ [-1; 0), то есть x < 0, то|a| <= x + 4 Из 2 неравенстваx^2 + 8x - 16(a+3) < 0D/4 = 4^2 + 16(a+3) = 16(a+4) = [4√(a+4)]^2x1 = -4 - 4√(a+4); x2 = -4 + 4√(a+4)Так как ветви параболы направлены вверх, то решение неравенства: x ∈ (x1; x2) = (-4 - 4√(a+4); -4 + 4√(a+4))Если хоть одно решение попадает в промежуток [-1; 0], то эти промежутки пересекаются. 1) { x1 = -4 - 4√(a+4) < -1{ x2 = -4 + 4√(a+4) >= -1Выделяем корень{ 4√(a+4) > -3 - это верно при любом а >= -4, т.к. корень арифметический.{ 4√(a+4) >= 3a+4 >= (3/4)^2a >= -4 + 9/16 = -55/16 = -3 7/162){ x1 = -4 - 4√(a+4) <= 0 - это верно при любом а >= -4{ x2 = -4 + 4√(a+4) >= 0Выделяем корень√(a+4) >= 1a + 4 >= 1a >= -3У меня получается a ∈ [-3; 4]Это, конечно, неправильно, но интересно, где я ошибся?