-
Помогите пожалуйста с неравенством изображенном на картинке
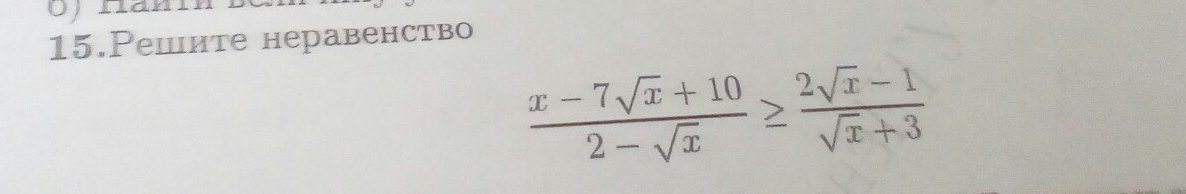
Ответы 1
-
(x - 7√x + 10) / (2-√x) ≥ (2√x -1)/(√x + 3)Одз x>=0 2-√х≠2 х≠4√x=t t≥0(t² - 7t + 10)/(2-t) - (2t-1)/(t+3) ≥ 0(t-2)(t-5)(t+3)/(2-t)(t+3) + (t-2)(2t-1)/(2-t)(t+3)≥0(t-2)(t²-2t-15+2t-1)/(t-2)(t+3)≤0 (поменяли 2-t на t-2)(t-2)(t²-16)/(t-2)(t+3) ≤ 0 (t-2)(t-4)(t+4)/(t-2)(t+3)≤0 так как t≥0 то можно выкинуть t+3 и t+4 они всегда будут больше 0(t-2)(t-4)/(t-2)≤0///////0---------2--------4+++++++t≥0√x≥0 x≥0t≤4√x≤4x≤16t≠2 √x≠2x≠4x∈[0 4) U (4 16]
-
Автор:
chaim - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите с переводомThe Diamond Club is a dating website which aims to pair male millionaires with physically attractive females. Male members pay upwards of £100,000 to join the site, while female members are ranked out of 100 for their physical attractiveness and do not pay a fee to join. No other qualities, such as skills or interests, are taken into account when ranking female members. The site is for linking of dates, and not for prostitution.Motion: feminists should not oppose dating sites which seek to romantically link rich men and physically attractive women.
artists should not set out to sympathetically portray characters who hold morally repugnant world views-
Предмет:
Английский язык -
Автор:
alvaroi8af - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Найди площадь прямоугольника, если известно, что 1/4 часть прямоугольника равна 6 см2
-
Предмет:
Математика -
Автор:
butterballf0ww - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дана правильная треугольная призма ABCA1B1C1, в основании которой лежит равносторонний треугольник.
Сторона треугольника AB = 2, высота AA1 = 3.
Дана точка К - середина стороны B1C1.
Строим плоскость AKC и получаем точку P - середину A1B1.
Требуется найти расстояние BH от точки B до этой плоскости APKC.
Отрезок BH на рисунке показан красным.
Как вообще решаются подобные задачи? И правильно ли я построил чертеж? -
Фосфор+крейда буде реакцiя чи нi? Якщо так, то напишiть будь ласка.
-
Предмет:
Химия -
Автор:
rafaelgriffith - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
