-
Дана правильная треугольная призма ABCA1B1C1, в основании которой лежит равносторонний треугольник.
Сторона треугольника AB = 2, высота AA1 = 3.
Дана точка К - середина стороны B1C1.
Строим плоскость AKC и получаем точку P - середину A1B1.
Требуется найти расстояние BH от точки B до этой плоскости APKC.
Отрезок BH на рисунке показан красным.
Как вообще решаются подобные задачи? И правильно ли я построил чертеж?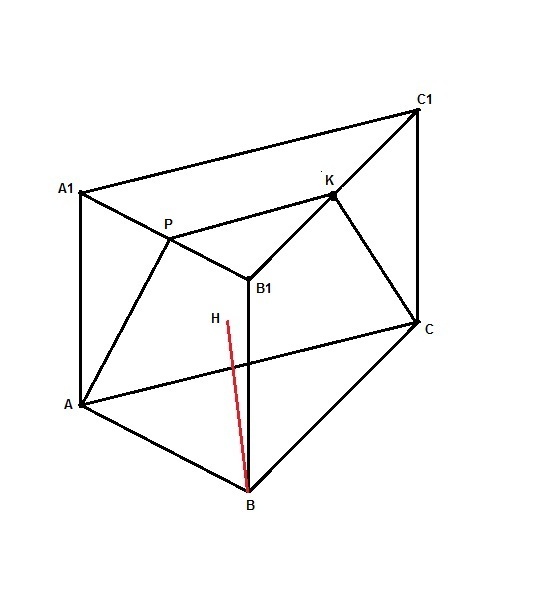
Ответы 6
-
к выше посчитано
-
Автор:
cierra - 6 лет назад
-
0
-
-
а, ну да, пропустил. Спасибо!
-
Автор:
keltonrowland - 6 лет назад
-
0
-
-
это стандартный путь по накатанной. один раз сделать - потом автоматом... у меня тут с пяток однотипных решений. координаты точек нужно только не забывать править )
-
Автор:
sweet-peateed - 6 лет назад
-
0
-
-
чем ихорошо. картинка всякий раз разная...
-
Автор:
wyattmorgan - 6 лет назад
-
0
-
-
https://znanija.com/task/24896809 Вот кстати , правда попроще задача, но решенная обоими методами.
-
Автор:
dominikuh4c - 6 лет назад
-
0
-
-
"дядя Вова - скрипач не нужен! " - чертёж то есть ) пусть А начало координат .ось x - AСось у - перпендикулярно АС в сторону В.ось z - AA1координаты интересующих точек С(2;0;0)К(1,5;√3/2;3)В(1;√3;0)уравнение плоскости АКС - проходит через 0.аx+by+cz=0подставляем координаты точек1.5а+√3/2b+3c=02a=0. a=0пусть b=1 тогда с= - 1/2√3y-z/2√3=0нормализованное уравнение плоскостик=√(1+1/12)=√(13/12)y/k-z/2√3k=0подставляем В в нормализованное уравнениерасстояние от В до АКС равно= √3/к=√36/√13= 6√13/13
-
Автор:
esmeralda4hem - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найди площадь прямоугольника, если известно, что 1/4 часть прямоугольника равна 6 см2
-
Предмет:
Математика -
Автор:
butterballf0ww - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Помогите пожалуйста с неравенством изображенном на картинке
-
Фосфор+крейда буде реакцiя чи нi? Якщо так, то напишiть будь ласка.
-
Предмет:
Химия -
Автор:
rafaelgriffith - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- корень из 3 на sinx-cosx=2
How much to ban the user?
1 hour
1 day
100 years
