Задать вопрос Регистрация
Помочь другим

  • избавьтесь от иррациональности в знаменателе дроби

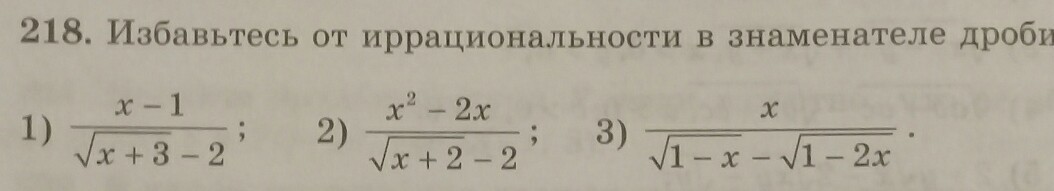
    question img

Ответы 1

  • Избавление от рациональности в знаменателе "лечится" умножением числителя и знаменателя на выражение, сопряжённое со знаменателем.1) \frac{x-1}{ \sqrt{x+3}-2} умножаем числитель и знаменатель на \sqrt{x+3}+2\frac{x-1}{ \sqrt{x+3}-2}=\frac{(x-1)*(\sqrt{x+3}+2)}{(\sqrt{x+3}-2)*(\sqrt{x+3}+2)}=\frac{(x-1)*(\sqrt{x+3}+2)}{x+3-4}=\sqrt{x+3}+22) \frac{ x^{2} -2x}{ \sqrt{x+2}-2} умножаем числитель и знаменатель \sqrt{x+2}+2 \frac{ x^{2} -2x}{ \sqrt{x+2}-2}= \frac{ (x^{2} -2x)*(\sqrt{x+2}+2)}{ (\sqrt{x+2}-2)*(\sqrt{x+2}+2)}=\frac{ x*(x -2)*(\sqrt{x+2}+2)}{ x+2-4}=x*(\sqrt{x+2}+2)3) \frac{x}{ \sqrt{1-x}- \sqrt{1-2x}} умножаем числитель и знаменатель на \sqrt{1-x}+ \sqrt{1-2x}\frac{x}{ \sqrt{1-x}- \sqrt{1-2x}}=\frac{x*(\sqrt{1-x}+ \sqrt{1-2x})}{ (\sqrt{1-x}- \sqrt{1-2x})*(\sqrt{1-x}+ \sqrt{1-2x})}= \\ \\ =\frac{x*(\sqrt{1-x}+ \sqrt{1-2x})}{ (1-x)- (1-2x)}=\frac{x*(\sqrt{1-x}+ \sqrt{1-2x})}{ 1-x-1+2x}=\sqrt{1-x}+ \sqrt{1-2x}

    • Автор:

      dillon
    • 4 года назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years