Задать вопрос Регистрация
Помочь другим

  • Исследовать функцию f(x) на непрерывность. Определить характер точек разрыва, если они существуют.

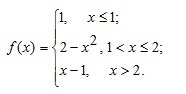
    question img

Ответы 1

  • Утверждение:Функция f непрерывна в \mathbb R\setminus \{2\}.Доказательство:Для всех x \leq 1, функция f является постоянной.Следовательно, для всех x_0\ \textless \ 1 выполняется:\displaystyle \lim_{x \to x_0} f(x)=1=f(x_0) Т.е. данная функция непрерывна в (-\infty,1).Докажем что,\displaystyle \lim_{x \to 1} f(x)=f(1)=1Для этого достаточно найти односторонние пределы: \displaystyle \lim_{x \to 1^-} f(x), \lim_{x \to 1^+} f(x)Для всех x\ \textless \ 1 выполняется f(x)=1, следовательно:\displaystyle \lim_{x \to 1^-} f(x) =1=f(1)Для всех 1\ \textless \ x \leq 2 выполняется f(x)=2-x^2, следовательно:\displaystyle \lim_{x \to 1^+} f(x) =\displaystyle \lim_{x \to 1^+} (2-x^2)=2-1=1=f(1)Отсюда следует:\displaystyle \lim_{x \to 1} f(x)=f(1)Следовательно, f непрерывна в x=1.Для всех x\ \textgreater \ 2, выполняется f(x)=x-1. Следовательно, для всех x_0 \in (2,+\infty) выполняется:\displaystyle \lim_{x \to x_0} f(x)= \lim_{x \to x_0} (x-1)=x_0-1=f(x_0)Т.е. f непрерывна в (2,+\infty).Таким же образом, f непрерывна в (1,2), т.к.:\displaystyle \lim_{x \to x_0} f(x)=\lim_{x \to x_0} (2-x^2)=2-x_0^2=f(x_0)Для всех x_0 \in (1,2).Теперь докажем что x_0=2 точка разрыва типа "скачок":Для всех 1\ \textless \ x\ \textless \ 2, f(x)=2-x^2 следовательно:\displaystyle \lim_{x \to 2^-}f(x)= \lim_{x \to 2^-} (2-x^2)=2-2^2=-2Однако, для всех x\ \textgreater \ 2, f(x)=x-1. Следовательно:\displaystyle \lim_{x \to 2^+}f(x)= \lim_{x \to 2^+}(x-1)=2-1=1Т.е. \displaystyle \lim_{x \to 2^+}f(x)e\lim_{x \to 2^-}f(x).В итоге, получаем что f непрерывна в \mathbb R \setminus\{2\}.Ч.Т.Д.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years