-
Тригонометрия (системы). Решите пожалуйста 647, по возможности 648. Спасибо!
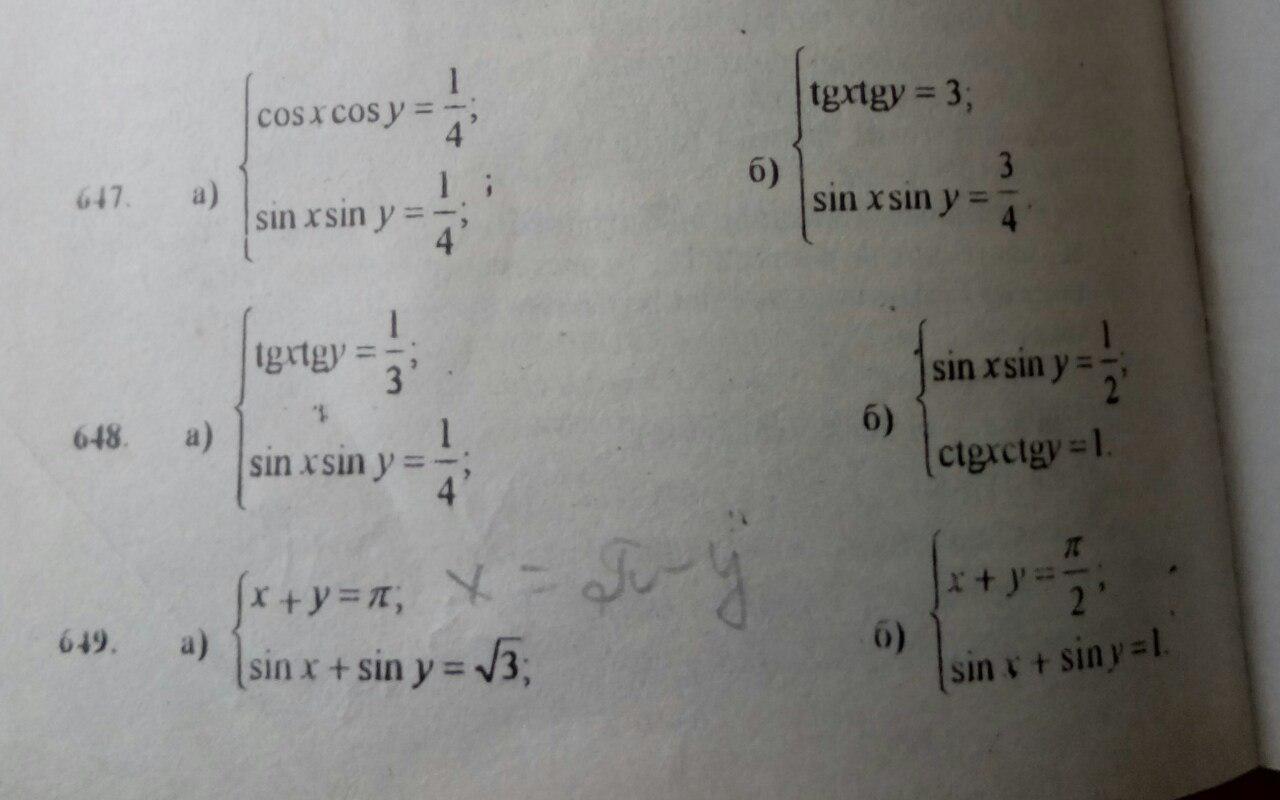
Ответы 2
-
спасибо) Вы меня не впервые выручаете))
-
Автор:
makaylazaaq - 6 лет назад
-
0
-
-
task/28423814-------------------647. а){ cosxcosy =1/4; { cosxcosy+sinxsiny =1/4+1/4 ; { cos(x-y) =1/2 ;< ⇔ < ⇔ < { sinxsiny = 1/4. { cosxcosy-sinxsiny =1/4-1/4. { cos(x+y) = 0.--- { x - y = ± π/3 +2πm , m ∈ ℤ < { x + y = π/2 +πl , l ∈ ℤ . ----------- a) { x - y = π/3 +2πm , m ∈ ℤ { 2x = (π/3+π/2) + πl+2πm , m,l ∈ ℤ< ⇔ < { x+y = π/2 +πl , l ∈ ℤ . { 2y = (π/2-π/3)+ πl -2πm, m,l ∈ ℤ . { x = 5π/12+ (l+2m )π/2 , m,l ∈ ℤ { x = 5π/12+(π/2)*k , k ∈ ℤ < ⇔ < { y = π/12 + (l - 2m)π/2, m,l ∈ ℤ . { y = π/12 +(π/2)*n, n ∈ ℤ .l+2m=k , l - 2m =n----------------- б) { x - y = - π/3 +2πm , m ∈ ℤ { 2x = (π/2 - π/3)+ πl+2πm , m,l ∈ ℤ< ⇔ < { x+ y = π/2 +πl , m ∈ ℤ . { 2y = (π/2 +π/3)+ πl - 2πm, m,l ∈ ℤ . { x = π/12+ (π/2)*(l+2m ) , m,l ∈ ℤ { x = π/12+ (π/2)*k , k ∈ ℤ < ⇔ < { y = 5π/12 + (π/2)*(l -2m), m,l ∈ ℤ . { y = 5π/12 +(π/2)*n , n ∈ ℤ .* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *647. б) {tgx*tgy =3 , { sinxsiny / cosxcosy = 3 , {cosxcosy =1/4 ,< ⇔ < ⇔ < || ± || ⇔ { sinxsiny =3/4. { sinxsiny =3/4. {sinxsiny = 3/4. --- {cosxcosy -sinxsiny =1/4-3/4, {cos(x+y) =-1/2, { x+y =±2π/3+2πm , m∈ ℤ < ⇔ < ⇔ < {cosxcosy +sinxsiny =1/4 + 3/4. {cos(x-y) =1. { x-y =2πl ,l ∈ ℤ --- {2x = ±2π/3 +2(m +l) , m,l ∈ ℤ { x = ±π/3+π(m+l) , m,l ∈ ℤ< ⇔ < { 2y = ±2π/3+2(m-l)π ,m,l ∈ ℤ . { y = ±π/3+π(m-l) , m,l ∈ ℤ . * * * m+l= k ∈ ℤ , m - l =n∈ ℤ . * * * { x = ±π/3+πk , k ∈ ℤ < { y =± π/3 + πn, n ∈ ℤ .-----------------
-
Автор:
harriet - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
20:(-33-4*(-7))-47= Помогите
-
Предмет:
Математика -
Автор:
kevinnelson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
На клеточном поле со стороной клетки 1 см изображён прямоугольник
1) Найди площадь этого прямоугольника
2) Проведи на рисунке прямую линию, которая разделит этот прямоугольник на два прямоугольника, так, чтобы периметр одного из них был равен 12 см
-
Предмет:
Математика -
Автор:
barbies9ye - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
На краю плавающей дощечки сидит лягушка массой 50 г. Насколько сместится
дощечка, если лягушка перепрыгнет на другой край дощечки? Масса дощечки 450 г, ее
длина 50 см. Сопротивлением движению пренебречь.-
Предмет:
Физика -
Автор:
velveti56m - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- log2(x+1)+log2(x+2)=3-log2 (4)
How much to ban the user?
1 hour
1 day
100 years
