-
Помогите! (отмечу как лутший) вычислите (розпишите детально)
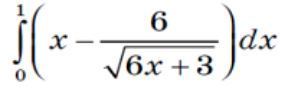
-
Предмет:
Алгебра -
Автор:
jabarityec - 6 лет назад
-
Ответы 1
-
Сначала найдём неопредплённый интеграл:∫(x - 6/sqrt(6x+3))dx = ∫xdx - 6∫dx/sqrt(6x+3)∫xdx = x^2/2 + C6∫dx/sqrt(6x+3)Внесём 6 под знак дифференциала∫d(6x)/sqrt(6x + 3)Добавим в дифференциале константу∫d(6x + 3)/sqrt(6x + 3) = ∫(6x + 3)^(-1/2)d(6x + 3) = 2sqrt(6x + 3) + CВычислим определённый интеграл:(x^2/2 - 2sqrt(6x + 3))|(0;1) = 1/2 - 6 + 2sqrt(3) = 2sqrt(3) - 11/2
-
Автор:
maleahavery - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Подставьте многочлен в виде произведения x в квадрате - xy - 4x + 4y.
-
Помогите найти адрес Ирвина в рассказе "Бурый волк"
-
Предмет:
Литература -
Автор:
greer - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
Сочинение на тему "Как помочь себе не начать курить"
-
Предмет:
Биология -
Автор:
dreameyfoxk - 6 лет назад
-
Ответов:
5 -
Смотреть
-
- Основные сословия 16 и 17 века в России. Сравнительная характеристика
How much to ban the user?
1 hour
1 day
100 years
