-
Найти угол в уравнении. 100 балов
[tex] h=tg(\alpha) *L-\frac{g*L^{2}}{2*v^{2}*cos(\alpha)^{2}} [/tex]
Уравнение сложное. Должно быть два значения.
Подсказка: Сведите задачу к квадратному уравнению относительно tgα, воспользовавшись основным тригонометрическим тождеством.
Пробовал свести - не получается.
На всякий случая прикладываю ответ (см. рисунок)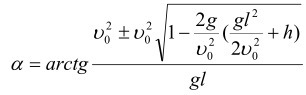
-
Предмет:
Алгебра -
Автор:
valentínhubbard - 6 лет назад
-
Ответы 4
-
Спасибо большое, вспомнил про 1/cos^2(a) в тот момент, как только Вы ответили )
-
Автор:
chiquitaeq3q - 6 лет назад
-
0
-
-
На пользу
-
Автор:
elainaharrington - 6 лет назад
-
0
-
-
Здравствуйте! Очень прошу посмотреть Мат. ожидание стратегия игры https://znanija.com/task/29274828
-
Автор:
fritz - 6 лет назад
-
0
-
-
Воспользовавшись тождеством 1+tg^2a=1/cos^2a Подставляя h=tga*L - g*L^2*(1+tg^2a)/(2v^2) Или (-g*L^2/(2v^2))*tg^2a + L*tga - (g*L^2/(2v^2)+h) = 0 Получили квадратное уравнение D=sqrt(L^2-(4*g*L^2/(2v^2))*(g*L^2/(2v^2)+h)) = L*sqrt(1-(2*g/v^2)*(g*L^2/(2v^2)+h)) tga=(-L+/- L*sqrt(1-(2*g/v^2)*(g*L^2/(2v^2)+h)))/(-g*L^2/v^2) Откуда сокращая на L , умножая числитель на v^2 , получаем требуемое
-
Автор:
hinton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
визначити енергію магнітного поля котушки що складається з 200 витків якщо при струму 4 ампера в ній виникає магнітний потік у 0,01 Вб
-
Предмет:
Физика -
Автор:
aedanbender - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- В основании прямой призмы лежит треугольник со сторонами 5,3 и 6 см. Высота призмы равна 10 см. Найти площадь поверхности и объем.
-
по графику функции изображённому на рисунке найдите значение функции при x=-3, x=2
пожалуйста)-
Предмет:
Алгебра -
Автор:
kylieparker - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Допишите ядерную реакцию:
?+1 1H --- 22 11Na + 4 2He
How much to ban the user?
1 hour
1 day
100 years
