Задать вопрос Регистрация
Помочь другим

  • Привет, помогите с системой уравнений.
    Заранее спасибо! Желательно примеры а и б .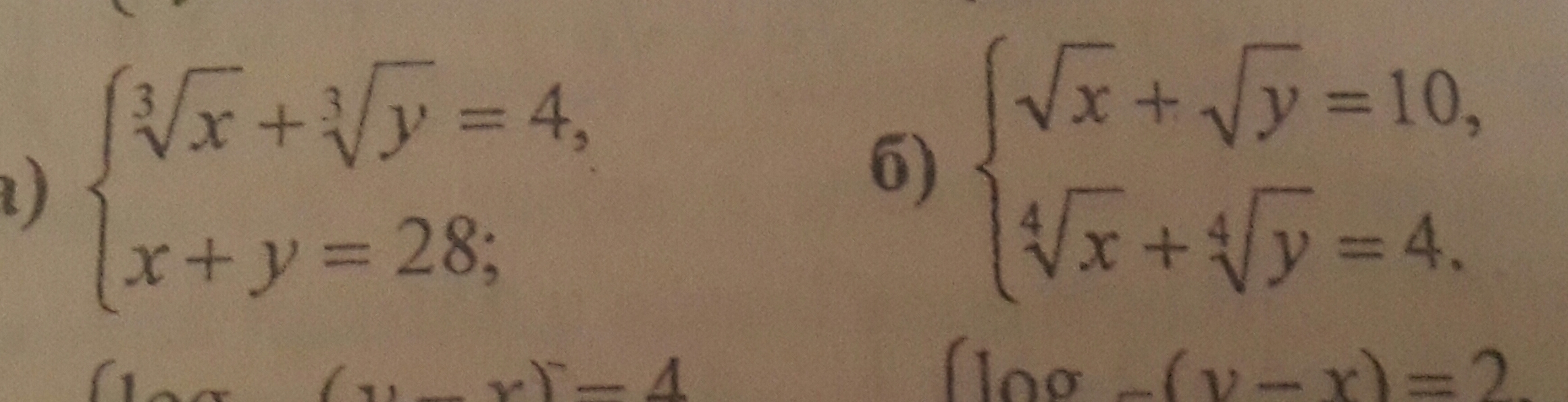

    question img

Ответы 1

  • а) \left \{ {{ \sqrt[3]{x}+ \sqrt[3]{y} =4} \atop {x+y=28}} ight. \left \{ {{( \sqrt[3]{x}+ \sqrt[3]{y})^{3} =(4)^{3}} \atop {x+y=28}} ight. \left \{ {{x+y+ 3\sqrt[3]{x} \sqrt[3]{y}(\sqrt[3]{x}+ \sqrt[3]{y} )=64} \atop {x+y=28}} ight. из за того, что x+y=28, а  \sqrt[3]{x} + \sqrt[3]{y}=4 , тогда \left \{ {{28+ 3\sqrt[3]{x} \sqrt[3]{y}*4=64} \atop {x+y=28}} ight. \left \{ {{12\sqrt[3]{xy}=64-28} \atop {x+y=28}} ight. \left \{ {{\sqrt[3]{xy}= \frac{36}{12} } \atop {x+y=28}} ight. \left \{ {{(\sqrt[3]{xy})^{3}= 3^{3}} \atop {x+y=28}} ight. \left \{ {xy= 27} \atop {x=28-y}} ight. (28-y)y=2728y-y²=27y²-28y+27=0D=28²-4·1·27=784-108=676=26²y₁= \frac{28-26}{2}= \frac{2}{2} =1 y₂= \frac{28+26}{2}= \frac{54}{2} =27 x₁=28-y₁=28-1=27x₂=28-y₂=28-27=1б) (\sqrt[4]{x})^{2} = a^{2}                     (\sqrt[4]{y})^{2} = b^{2} \sqrt{x} =a^{2}                               \sqrt{y} =b^{2}  \left \{ {{ a^{2}+ b^{2} =10} \atop {a+b=4}} ight. \left \{ {{ a^{2}+b^{2}=10} \atop {a=4-b}} ight. (4-b)²+b²=1016-8b+b²+b²-10=02b²-8b+6=0                 (:2)b²-4b+3=0D=16-12=4=2²b₁= \frac{4-2}{2} = \frac{2}{2}=1 b₂= \frac{4+2}{2} = \frac{6}{2} =3a₁=4-1=3a₂=4-3=1 (\sqrt{x})^{2} = (a^{2} )^{2}x=a⁴( \sqrt{y})^{2} = (b^{2})^{2} y=b⁴x₁=a₁⁴=3⁴=81y₁=b₁⁴=1⁴=1x₂=a₂⁴=1⁴=1y₂=b₂⁴=3⁴=81

    • Автор:

      aidynptaq
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years