-
Как мы тут получаем выделенное снизу значение? То что написал внутри квадрата это формула и по формуле не должно быть перед е 1/4 ← как вообше это получаем?
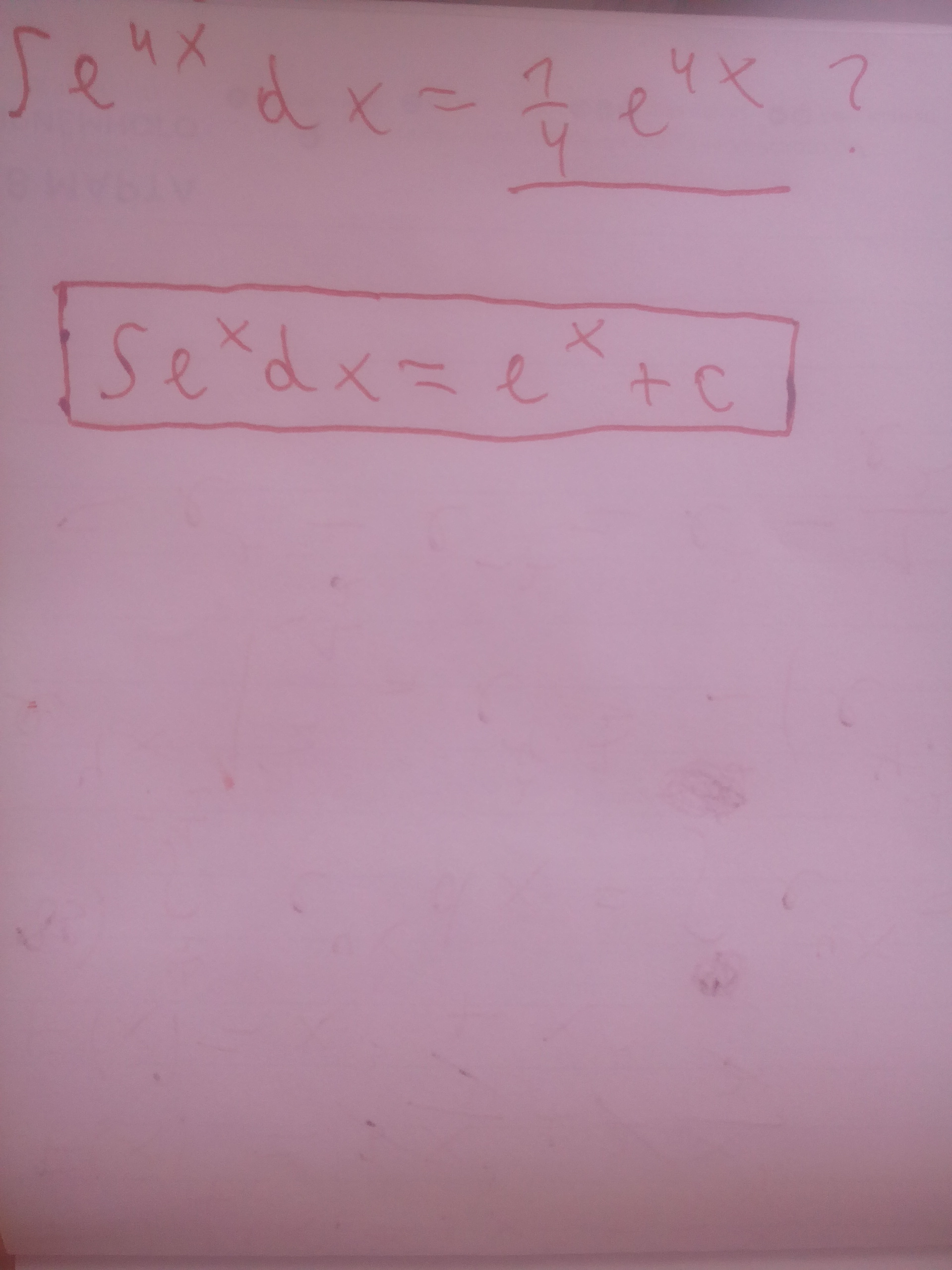
Ответы 8
-
в случае с 4e^(4x) по dx проблема в том, что у вас интеграл не тот. я показала, что первообразная e^(4x) не дает тот интеграл, который вам нужен
-
Автор:
cali1ga1 - 6 лет назад
-
0
-
-
пределы интегрирования? сейчас не важно, сначала решаем неопределенный интеграл
-
Автор:
patty1utx - 6 лет назад
-
0
-
-
Я вам сейчас скину ссылку на задание.
-
Автор:
french - 6 лет назад
-
0
-
-
https://znanija.com/task/29298694
-
Автор:
brooksnash - 6 лет назад
-
0
-
-
https://znanija.com/task/29299041
-
Автор:
parkersimmons - 6 лет назад
-
0
-
-
https://znanija.com/task/29299041
-
Автор:
damarisnxrr - 6 лет назад
-
0
-
-
∫(e^(4x))dx = (1/4)*∫(e^t)dt = (1/4)* e^t +C = (1/4)* e^(4x) +C4x = t4dx = dtdx = (1/4)dt
-
Автор:
alysonconner - 6 лет назад
-
0
-
-
Функция y =
- сложная, значит, ее производная берется так: y' =
Значит, интеграл будет такой:
Вам же эта четверка не нужна. Поэтому, чтобы от нее избавиться, нужно к первообразной функции добавить
y =
*
, y' =
* 4 *
=
- то, что нужно. Значит,
И Вы забыли добавить константу! Больше не забывайте. То есть нужно помнить, что Ваша функция - сложная, поэтому нужно избавляться еще и от 4. Просто попробуйте продифференцировать получившуюся функцию обратно - и поймете, что Ваш результат не совпадет с нужным. Надеюсь, что стало чуть-чуть понятнее, если что, готова ответить в комментариях.
-
Автор:
alison - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите плиз
1) 70-a=70:2
2) 420-c=120*3
3)k*380=240:4
4)x+15=100:4-
Предмет:
Математика -
Автор:
theodoreyqi6 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Найдите значение тангенса , если известно что cos a=4/5, a€1 четвети
-
Предмет:
Алгебра -
Автор:
dannachang - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите рассчитать
-0,403 + 0,059/2*lg0,8=
0,799+0,059/1*lg0,01= -
Какие мысли и чувства вызывает произведение Гоголя Вечер наканупе Ивана купала
-
Предмет:
Литература -
Автор:
kikiubie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
