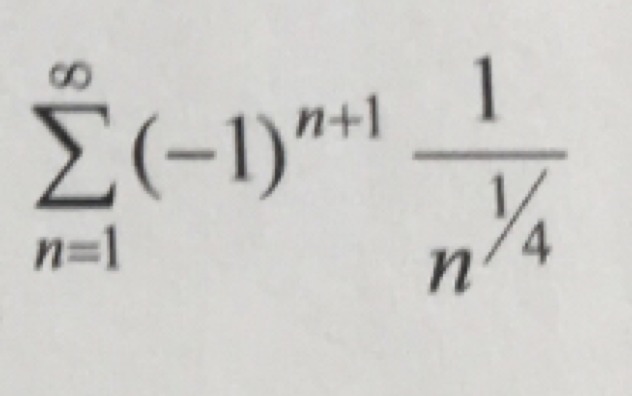Ответы 1
-
1. Первое условие признака Лейбница выполняется, т.е.
каждый последующий член ряда меньше предыдущего
По признаку Лейбница ряд сходится.
Проверим теперь на абсолютность сходимости ряда, взяв ряд по модулю
И этот ряд расходится, следовательно данный ряд сходится условно.
-
Автор:
elsaknox - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
выберите верное утверждение. азотистая кислота в окислительно-восстановительных
-
Предмет:
Химия -
Автор:
jaguarsolis - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ДАЮ 50 Баллов!
Найдите наибольшее и наименьшее значение функции
f(x) = х^3 - 3х^2 +1 на отрезке [1:3]-
Предмет:
Математика -
Автор:
nemesio - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Радиус основания цилиндра 2 см, площадь боковой поверхности вдвое больше площади основания. НАЙДИТЕ ОБЪЕМ ЦИЛИНДРА
-
Предмет:
Математика -
Автор:
baxterflot - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Исследовать на абсолютную и условную сходимость ряд:
How much to ban the user?
1 hour
1 day
100 years