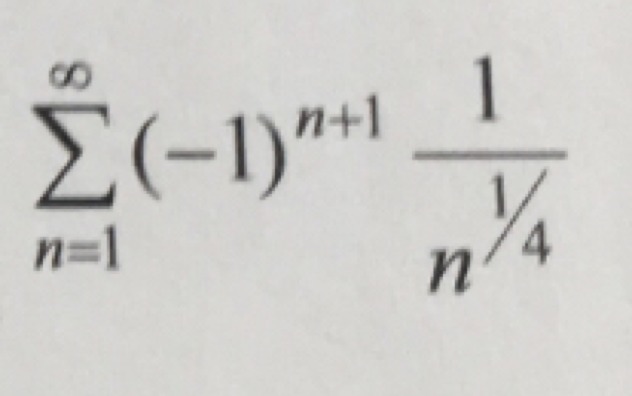Ответы 2
-
Ряд сходится условно, т.к. все условия признака Лейбница выполняются, а ряд составленный из абсолютных величин является обобщённо гармоническим расходящимся рядом.
-
Автор:
jamievmz5 - 6 лет назад
-
0
-
-
1. Первое условие признака Лейбница выполняется, т.е.
каждый последующий член ряда меньше предыдущего
По признаку Лейбница ряд сходится.
Проверим теперь на абсолютность сходимости ряда, взяв ряд по модулю
И этот ряд расходится, следовательно данный ряд сходится условно.
-
Автор:
gross - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Исследовать на абсолютную и условную сходимость ряд:
-
Радиус основания цилиндра 2 см, площадь боковой поверхности вдвое больше площади основания. НАЙДИТЕ ОБЪЕМ ЦИЛИНДРА
-
Предмет:
Математика -
Автор:
baxterflot - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как узнать частотность букв в Русском языке,(учусь в 4 классе,просто очень надо,объяснять конкретно
-
Предмет:
Другие предметы -
Автор:
luciapowers - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
выпишите из Конституции РФ (статьи № 2, 3, 6, 7, 10, 13, 29, 30, 32) положения, подтверждающие признаки демократии.
-
Предмет:
Обществознание -
Автор:
apple jackc6ra - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years