Задать вопрос Регистрация
Помочь другим

  • спасайте, надо исследовать эту функцию. и объясните, пожалуйста, куда смещать/отображать график исходной функции при построении

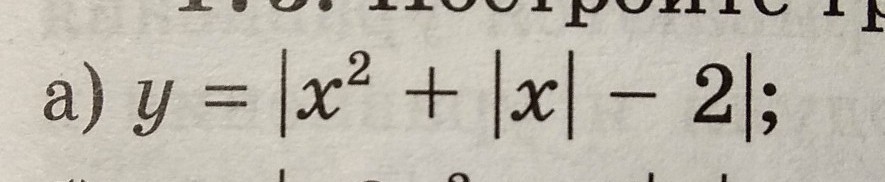
    question img

Ответы 1

  • y(x) = | {x}^{2} + |x| - 2 | = \\ = | { |x| }^{2} + |x| - 2 | так как| - x| = |( - 1) \cdot x| = \\ = | - 1| \cdot |x| = 1 \cdot |x| = |x| то y( - x) = | { | - x| }^{2} + | - x| - 2 | = \\ = | { |x| }^{2} + |x| - 2 | = y(x) \\ функция чётнаяфункция определена для всех хDy:x€RЕу:[0,+∞)то есть функция ограничена , она принимает только неотрицательные значения (из-за свойств модуля)и принимает вид:y(x) = \left \{ {{x \geqslant 0... = | {x}^{2} + x - 2 | } \atop {x < 0... = | {x}^{2} - x - 2 |}} ight. \\ каждый из этих промежутков разбивается ещё на два (см фото)при x≥0x²+x-2≥0(x-1)(x+2)≥0[0,1)v[1;+∞)при x<0х²-х-2≥0(х-2)(х+1)≥0(-∞;-1]v(-1;0)функция будет иметь следующий видна этих промежуткахy(x) = \left \{ {{\left \{ {{(x \geqslant 1) = {x}^{2} + x - 2} \atop {(1 > x \geqslant 0) = - ({x}^{2} + x - 2)}} ight. } \atop {\left \{ {{(0 > x \geqslant - 1)= {x}^{2} - x - 2} \atop {( - 1 > x ) = - ({x}^{2} - x - 2)}} ight.}} ight. \\ у(х)=|f(x)|≥0, поэтому решим у(х)=0 | { |x| }^{2} + |x| - 2 | = 0 \\ { |x| }^{2} + |x| - 2 = 0 \\ ( |x| - 1)( |x| + 2) = 0 \\ |x| = 1 \\ x_1 = 1 \\ x_2 = - 1 \\ при х¹'²=±1 ( кстати, это нули функции), функция примет наименьшее значение =0yнаибольшее =+∞ график на рисунке
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years