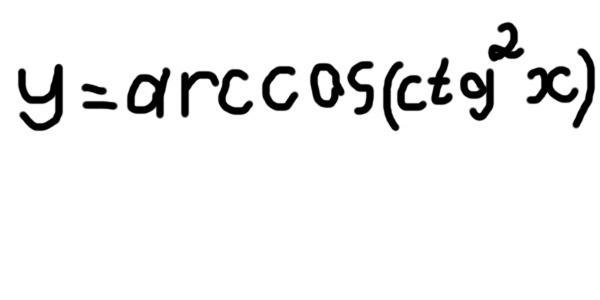Ответы 2
-
-
Автор:
capricebr9t - 6 лет назад
-
0
-
-
-
Автор:
aiden272 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Составьте таблицу «Причины крестовых походов». Пожалуйста!!!
Что хотели получить? Что получили после 1 кр похода?
Все христиане
Феодалы
Крестьяне
Духовенство -
f(x)= x^3-5x^2+1 .Найдите уравнение касательной к графику функции f в точке пересечения графика функции f с осью ординат
-
Предмет:
Математика -
Автор:
chucklesuenr - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Я задаю себе вопросы:
Что я хочу? и Что я могу?
На вопрос "что я хочу", я могу ответить. Например: Изучить ино. языки, путешествовать, познать космос, построить себе достойную жизнь.
А вот на вопрос "что я могу", я просто ухожу в закат. (В свои 16 лет) У меня нет голоса, что бы красиво петь, я плохо рисую, я не умею играть на инструментах, плохо танцую, я плохо владею даже английским яз., тд. Понимаю, ..что никогда не поздно.., но так у меня сложилось. По мне уже поздно, вот честно...
Вот смотрю разные программы, и восхищаюсь талантливыми людьми, а потом грусть...
Да, что ещё в час ночи можно написать...
Жду умные комменты по типу - мнмттпврнлтмакмтггтикыч(нет)-
Предмет:
Психология -
Автор:
humbertogiles - 6 лет назад
-
Ответов:
3 -
Смотреть
-
- (x^(2)-4)/10>(x-2)^lg(x+2)
How much to ban the user?
1 hour
1 day
100 years