Задать вопрос Регистрация
Помочь другим

  • Неравенство с модулем
    Решение с объяснением пожалуйста.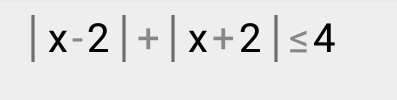

    question img

Ответы 1

  • Раскрытие модуля по определению делается следующим образом:

    | f(x) | = g(x) , это какие-то функции от аргумента х. Если f(x) не отрицательное, тогда модуль не изменит знак и | f(x) | = f(x). Если f(x) отрицательно тогда -f(x) это положительное число, значит | f(x) | = -f(x).

    "если" это условие значит будет пересечение значений, то есть фигурная скобка. А эти два получившихся значения будут решением одновременно, то есть квадратная скобка. Далее решение.

    \left[\begin{array}{ccc}\left \{ {{x-2\geq 0} \atop {x-2+|x+2|\leq 0}} ight. \\\left \{ {{x-2<0} \atop {-x+2+|x+2|\leq 0}} ight. \\\end{array}

    \left[\begin{array}{ccc}\left \{ {{x\geq 2} \atop {\left[\begin{array}{ccc}\left \{ {{x+2\geq 0}} \atop {x-2+x+2\leq 4} ight. \\\left \{ {{x+2<0} \atop {x-2-x-2\leq 4}} ight. \\\end{array} }} ight. \\\left \{ {{x<2} \atop {\left[\begin{array}{ccc}\left \{ {{x+2\geq 0} \atop {-x+2+x+2\leq 4}} ight. \\\left \{ {{x+2<0} \atop {-x+2-x-2\leq 4}} ight. \\\end{array} }} ight. \\\end{array}

    7.\left[\begin{array}{ccc}5.\left \{ {{x\geq 2} \atop {\left[\begin{array}{ccc}1.\left \{ {{x\geq -2}} \atop {x\leq 2} ight. \\2.\left \{ {{x<-2} \atop {-4\leq 4}} ight. \\\end{array} }} ight. \\6.\left \{ {{x<2} \atop {\left[\begin{array}{ccc}3.\left \{ {{x\geq -2} \atop {4\leq 4}} ight. \\4.\left \{ {{x<-2} \atop {x\geq  2}} ight. \\\end{array} }} ight. \\\end{array}

    Ответ: x∈[-2;2].

    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years