-
ПОЖАЛУЙСТА РЕШИТЕ,ОЧЕНЬ НАДО
Ответ должен быть (2; 2+√3], а у меня не получается (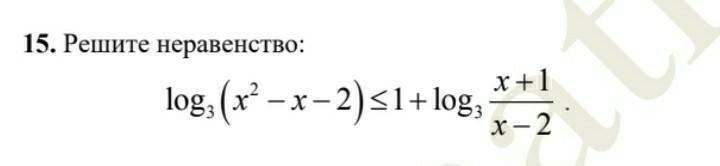
-
Предмет:
Алгебра -
Автор:
bridgerbzz - 6 лет назад
-
Ответы 5
-
Спасибо большое )
-
Автор:
savannahr8jm - 6 лет назад
-
0
-
-
Пожалуйста )
-
Автор:
geniusgg40 - 6 лет назад
-
0
-
-
Здравствуйте; помогите, пожалуйста, решить примеры по математике в профиле
-
Автор:
eliaefo - 6 лет назад
-
0
-
-
ОДЗ :
1) x² - x - 2 > 0
(x - 2)(x + 1) > 0
+ - +
_________₀__________₀___________
- 1 2
//////////////////// ////////////////////////
x ∈ (- ∞ ; - 1) ∪ (2 , + ∞)
2) (x + 1)(x - 2) > 0
Аналогично 1)
+ - + - +
_______[-1]________[2-√3]_________(2)________[2+√3]_______
/////////////////////// /////////////////////////
x ∈ [- 1 ; 2 - √3] ∪ (2 ; 2 + √3]
С учётом ОДЗ, окончательный ответ :
x ∈ (2 ; 2 + √3]
-
Автор:
jonah - 6 лет назад
-
0
-
-
Решение задания приложено

-
Автор:
ferrera8ii - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Показатель преломления вещества зависит от:
1)длины(частоты) световой волны
2)плотности среды
3)объема среды
4)направление распространения света в среде -
ученик сделал 9 деталей меньше, чем мастер . сколько деталей сделал каждый ,если ученик сделал 5/8того,что сделал мастер
помогите 5класс-
Предмет:
Математика -
Автор:
daniel91 - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Найдите последнюю цифру числа 317 в 49 степени.
С объяснением пожалуйста. -
Розв'яжіть задачу
Снігохід, маса якого разом з водієм становить 350 кг, рівномірно їде по горизонтальній поверхні. Яку силу тяги він розвиває, якщо коефіцієнт тяги дорівнює 0,1?
