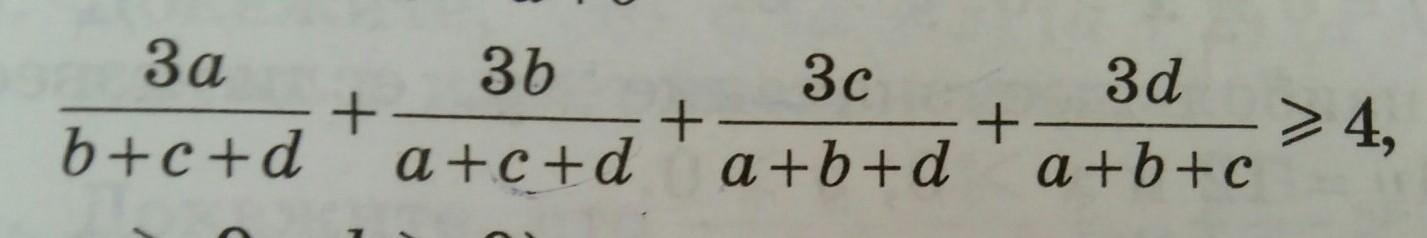докажите неравенство при a>0; b>0; c>0; d>0

блин

но это не доказательство

Понимаю тебя, доказательства фактически нет. Просто я не представляю как найти минимум без неравенства Коши. С этим неравенством всё однозначно. Ты его знаешь?

Так, я запутался. Если мы нашли минимум выражения и значение, при котором он достигается, то логично, что мы должны подставить это значение, иначе значение выражения будет больше. Отсюда a/d=1 и 1+(3a/d)=1+3=4. При других условиях(Например, если a не равно d), мы получим более большое значение выражения

Я не понимаю, что здесь надо ещё доказывать просто)

Пусть, для определённости, d>=c>=b>=a. Тогда всю дробь можно переписать в виде:

Что и требовалось доказать.

Пояснение: Выражение после первого знака неравенства получается, если взять наименьший знаменатель, а это d+d+d=3d.

Выражение после второго знака неравенства получается оттого, что мы берём наибольший числитель(то есть b+c+a=a+a+a=3a).

Выражение после третьего знака неравенства справедливо так как a>=d, то есть a/d>=1. Отсюда 3*(a/d)>=1*3=3

P.S. Если что-то непонятно, то не стесняйся спрашивать)