-
Решите неравенства:
a) ㏒₇ (2 - x) ≤ ㏒₇ (2x² - x)
б) ㏒₁/₂(x² - 1) < - 3
в) lg(7⁶⁻²ˣ+3) - lg39 > lg4 - 1g3
г) ㏒₂ₓ₊₁⁽⁵⁻²ˣ⁾ >1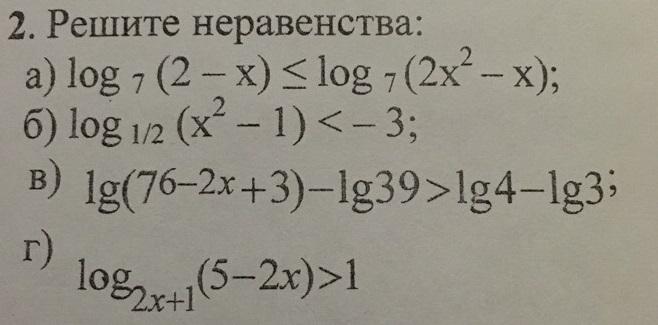
Ответы 1
-
N1
log 7 (2 - x) =< log 7 (2x^2 - x)
2 - x =< 2x^2 - x
2x^2 - 2 >= 0
x € (-беск. ; -1] U [1 ; +беск.)
N2
log 0,5 (x^2 - 1) < -3
log 0,5 (x^2 - 1) < log 0,5 (8)
x^2 - 1 > 8
x^2 - 9 > 0
x € (-беск. ; -3) U (3 ; +беск.)
N3
lg (7^(6 - 2x) + 3) - lg (39) > lg (4) - lg (3)
lg (7^(6 - 2x) + 3) > lg (39) + lg (4) - lg (3)
lg (7^(6 - 2x) + 3) > lg (52)
7^(6x - 2) + 3 > 52
7^(6x - 2) > 49
6x - 2 > 2
6x > 4
x > 2/3
N4
log 2x + 1 (5 - 2x) > 1
log 2x + 1 (5 - 2x) > log 2x + 1 (2x + 1)
5 - 2x > 2x + 1
- 4x > - 4
x < 1
log 2x + 1 (5 - 2x) > 1
log 2x + 1 (5 - 2x) > log 2x + 1 (2x + 1)
5 - 2x < 2x + 1
-4x < -4
x > 1
2x + 1 > 0
x € (-1/2 ; 0)
5 - 2x > 0
x € (0 ; 5/2)
{x € (-1/2 ; 0) x - не существует
{x > 1
{x € (0 ; 5/2) x € (0 ; 1)
{x < 1
Ответ : (0 ; 1
-
Автор:
kadenceqko8 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Каждый звук - шорох птицы, шелест упавшего листа - кажется громким, заставляет опасливо вздрогнуть.
Объясните, почему в данном предложении после слова "звук" стоит тире, а не двоеточие? И почему после слова "листа" - мы ставим тире-
Предмет:
Русский язык -
Автор:
happytparsons - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите площадь фигуры ограниченой линиями y=4-x² y=x+2. Если можете то напишите обьяснение что окуда взялось, а то я никак не разберусь
-
Предмет:
Алгебра -
Автор:
chynamendez - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
Чем наречие отличается от слов категории состояния?
Выберите один ответ:
a. Наличием форм степеней сравнения
b. Правописанием окончаний
c. Лексическим значением, синтаксической ролью;
d. Наличием форм мужского и женского рода-
Предмет:
Русский язык -
Автор:
luisamglm - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Найдите наименьшее натуральное число кратное 99, десятичная запись которого не содержит никаких цифр кроме единиц и нулей
Помогите пожалуйста-
Предмет:
Математика -
Автор:
perez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
