Задать вопрос Регистрация
Помочь другим

  • Найдите частное решение дифференциального уравнения, удовлетворяющее начальному условию. Заранее спасибо.

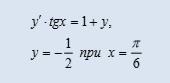
    question img

Ответы 1

  • \frac{dy}{dx} *\frac{sinx}{cosx} =1+y\\ \\ \int\frac{dy}{1+y} =\int\frac{cosx}{sinx}dx\\ \\ \ln|1+y|=\int\frac{d(sinx)}{sinx}\\ \\ \ln|1+y|=\ln|sinx|+\ln|C| \\ \\ 1+y=Csinx \\ y=Csinx-1 \\ \\ |y(\frac{\pi}{6})=-\frac{1}{2}| \\ \\ -\frac{1}{2}=Csin\frac{\pi}{6}-1 \\ \\ -\frac{1}{2}=C*\frac{1}{2}-1\ \ |*2 \\ \\ -1=C-2 \\ C=1 \\ \\ OTBET: \ y=sinx-1

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years