-
Найти наибольшее значение параметра 'a', при котором уравнение:
x^2-5x+6+sqrt(ax-2a)*(x-3)-6ax+18a=0 имеет единственное решение.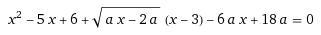
Ответы 11
-
А наибольшее значение а чему равно?
-
Автор:
ambrosio - 6 лет назад
-
0
-
-
получается что нет наибольшего
-
Автор:
arcadioy6uv - 6 лет назад
-
0
-
-
Смотрите, автору все равно, сама хочу разобраться. Но вижу, что два разных ответа, у вас и ниже. И между вами нет дискуссии. У меня пока выходит наибольшее а =1/4, х=3. Когда я записала уравнение (ваша третья строчка), то рассуждала так 0*0=0, х-3=0, х=3, подставила во вторую строчку и получила а=1/4. Так как вопрос "наибольшее", то рассматривать случай когда х=/3 и а=0, а<0 нет смысла, так как уже а=1/4>0. Теперь нужно бы рассмотреть случай когда а>0. Здесь остановилась. Ваше мнение?
-
Автор:
henryharrington - 6 лет назад
-
0
-
-
Посмотрите пожалуйста мой клиент выше, под другим ответом. Ваше мнение?
-
Автор:
luiscooper - 6 лет назад
-
0
-
-
я же написал что если а>0 и х≥2 то корнем является х=3. Тогда квадратное уравнение относительно √(x-2) должно быть решений не имеет или корни не удовлетворяют ОДЗ. Далее предположим что х= 3 не является корнем уравнения. Тогда остается лишь решить тот квадратное уравнение
-
Автор:
roccos7i4 - 6 лет назад
-
0
-
-
но для a>0 уравнение имеет 2 корня
-
Автор:
quinnupyx - 6 лет назад
-
0
-
-
Неверно, выразился. При a < 0 и a = 1/4 уравнение имеет единственное решение
-
Автор:
preston348 - 6 лет назад
-
0
-
-
Комент"
-
Автор:
alyvia - 6 лет назад
-
0
-
-
Да, спасибо. Т.е. наибольшее а=1/4 и будет ответом получается.
-
Автор:
constanciomcdonald - 6 лет назад
-
0
-
-
Если х =3 , то, подставляя в уравнение, получим a = 1/4
- квадратное уравнение относительно
Уравнение
решений не имеет для
При
уравнение имеет единственное решение. Наибольшее a = 1/4
-
Автор:
cindergilbert - 6 лет назад
-
0
-
-
Ответ:
Объяснение:
вынесем за скобки общие множители
x²-5x+6+[√(a(x-2))](x=3)-6a(x-3)=0 (1)
x²-5x+6 разложим на множители
х₁=-2;x=3 нашел подбором с использованием теоремы Виета
1. при а=0 выражение (1) принимает вид x²-5x+6=0 и имеет два решения
по формуле ax²+bx+c=a(x-x₁)(x-x₂)
x²-5x+6=(x+2)(x-3) подставим в (1)
(x+2)(x-3)+[√(a(x-2))](x=3)-6a(x-3)=0 вынесем за скобки общий множитель
(x-3)(x+2)+[√(a(x-2))]-6a)=0 это выражение имеет решение х=3
очевидно что, чтобы выражение (1) имело единственное решение выражение x+2+[√(a(x-2))]-6a=0 (2) не должно иметь решений
преобразуем выражение (2)
√(a(x-2))=-х+(6a-2) решим это уравнение графическим способом
у=√(a(x-2))
у=-х+(6a-2)
чтобы уравнение (2) не имело решений надо найти такое а при котором графики указанных выше функций не пересекались
выясним взаимное расположение графиков в зависимости от параметра а
2. При а>0
графиком у=√(a(x-2)) является кривая линия получающаяся из линии у=√х c помощью переноса вдоль оси ОХ на 2 единицы вправо и сжатием - растяжением вдоль оси ОХ в зависимости от значения а
крайняя левая по оси ОХ точка кривой (2;0) , ветка кривой направлена вправо .
так как a>0 (6a-2)>-2
2.1. при (6a-2)=2 прямая у=-х+(6a-2) имеет вид у=-х+2 и проходит через точку (2;0) и графики пересекаются в этой точке, при этом (2) имеет одно решение
2.2 при 6a-2>2 прямая у=-х+(6a-2) находится выше прямой у=-х+2 и и графики пересекаются в двух точках при этом (2) имеет 2 решения
2.3 при 6a-2<2 прямая у=-х+(6a-2) находится ниже прямой у=-х+2 и и графики не пересекаются (2) не имеет решений
при этом
6a-2<2 ; 6a<4; a<4/6; a<2/3 с учетом того что мы рассматриваем a>0
0<a<2/3
3. При а<0
графиком у=√(a(x-2)) является кривая линия получающаяся из линии у=√х c помощью переноса вдоль оси ОХ на 2 единицы вправо и сжатием - растяжением вдоль оси ОХ в зависимости от значения а
крайняя правая относительно оси ОХ точка кривой (2;0) , ветка кривой направлена влево .
так как a<0 то (6a-2)<-2
так как (6a-2)<-2
прямая у=-х+(6a-2) в этом случае находится ниже прямой у=-х-2
которая имеет с графиком кривой общую точку и тоже имеет с графиком кривой общую точку
в этом случае (2) имеет решение
таким образом, уравнение 1 имеет единственное решение
при 0<a<2/3

-
Автор:
dominikuh4c - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Решите систему неравенств !!! Пожалуйста помогите !
-
Предмет:
Математика -
Автор:
buzzdvhk - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите плз даю 15 баллов!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Кожа, как стена дома, предохраняет наш организм от воздействия неблагоприятных факторов окружающей среды. Продолжите это сравнение по строению, свойствам и функциям. Каждое предложение начинайте словами «как и стена дома, кожа …» или «в отличие от стены, кожа…» Напишите не менее пяти предложений. -
Найти экстремум функции двух переменных. Заранее спасибо.
-
определите размер пословицы без беды друга не узнаешь: а) 22 байта, б)208 бит, в)0,01 Кбайт, г)26 бит
-
Предмет:
Информатика -
Автор:
shaniyabartlett - 6 лет назад
-
Ответов:
1 -
Смотреть
-
