Задать вопрос Регистрация
Помочь другим

  • Найти экстремум функции двух переменных. Заранее спасибо.

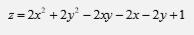
    question img

Ответы 1

  • Найдем частные производные по переменным x, y:

    \displaystyle \frac{\partial z}{\partial x}=2\cdot 2x-2y-2=4x-2y-2\\ \\ \frac{\partial z}{\partial y}=2\cdot 2y-2x-2=4y-2x-2

    Приравниваем частные производные к нулю:

    \displaystyle \left \{ {{4x-2y-2=0} \atop {4y-2x-2=0}} ight. ~~~\Rightarrow~~~~+\left \{ {{4x-2y-2=0} \atop {8y-4x-4=0}} ight. \\ \\ 8y-2y-2-4=0\\ 6y=6\\ y=1\\ \\ x=2y-1=2\cdot 1-1=1

    Вычислим теперь частные производные второго порядка для построения матрицы Гессиана:

    \displaystyle \frac{\partial^2z}{\partial x^2}=4;~~~~~~~\frac{\partial^2z}{\partial y^2}=4;~~~~~~\frac{\partial^2z}{\partial x\partial y}=-2

    \displaystyle \left(\begin{array}{ccc}4&-2\\ -2&4\end{array}ight)\\ \\ з_1=4>0\\ \\ з_2=\left|\begin{array}{ccc}4&-2\\ -2&4\end{array}ight|=4\cdot 4-(-2)\cdot (-2)=16-4=12>0

    В точке (1;-1) имеется минимум z(1;-1)=2\cdot 1^2+2\cdot (-1)^2-2\cdot 1\cdot(-1)-2\cdot 1-2\cdot (-1)+1=-1

    • Автор:

      loganbond
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years