Задать вопрос Регистрация
Помочь другим

  • Доказать, что при всех допустимых значениях a справедливо равенство.

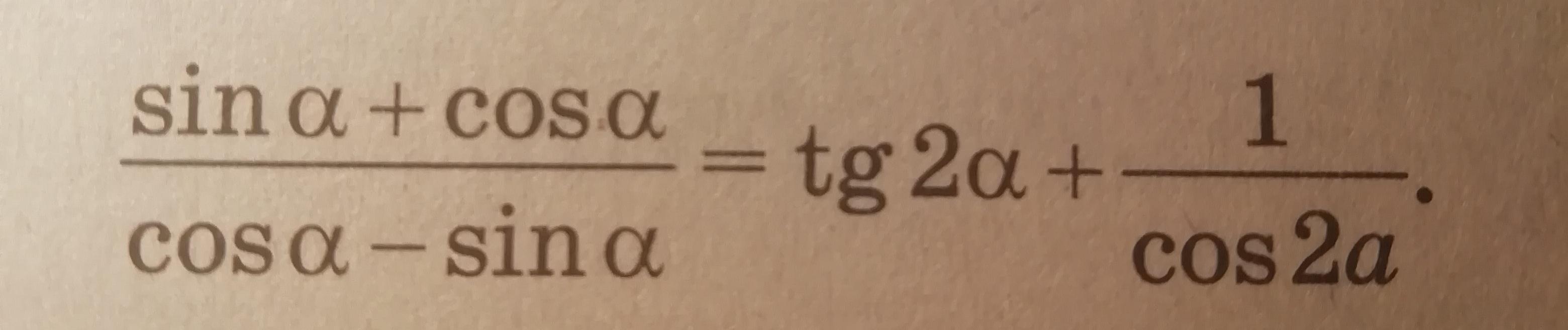
    question img

Ответы 2

  • Умножим числитель и знаменатель дроби на cosa + sina, получим:

    \displaystyle \frac{\sin \alpha+\cos\alpha}{\cos\alpha-\sin\alpha}=\frac{(\sin\alpha+\cos\alpha)^2}{(\cos\alpha-\sin\alpha)(\cos\alpha+\sin\alpha)}=\frac{1+\sin2\alpha}{\cos2\alpha}={m tg}2\alpha+\frac{1}{\cos2\alpha}

  • Преобразуем правую часть тождества :

    tg2\alpha+\frac{1}{Cos2\alpha}=\frac{Sin2\alpha}{Cos2\alpha}+\frac{1}{Cos2\alpha}=\frac{Sin2\alpha+1 }{Cos2\alpha}=\frac{Cos^{2}\alpha+2Sin\alpha Cos\alpha+Sin^{2}\alpha}{Cos^{2}\alpha-Sin^{2}\alpha}=\frac{(Cos\alpha+Sin\alpha)^{2}}{(Cos\alpha+Sin\alpha)(Cos\alpha-Sin\alpha)}=\frac{Sin\alpha+Cos\alpha}{Cos\alpha-Sin\alpha}\\\\\frac{Sin\alpha+Cos\alpha}{Cos\alpha-Sin\alpha}=\frac{Sin\alpha+Cos\alpha}{Cos\alpha-Sin\alpha}

    Тождество доказано

    • Автор:

      weaver55
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years