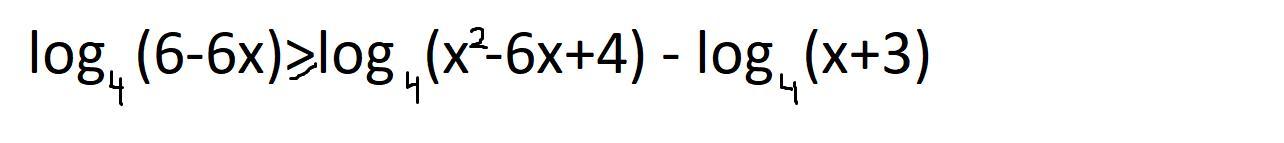Ответы 3
-
забыл у зелённого интервала убрать ветви параболы внизу /:
-
Автор:
freeman73 - 6 лет назад
-
0
-
-
Если что в третьем переходе (при решении системы), я сразу нашёл пересечение неравенств (границы которых уже были известны), чтобы не таскать за собой длинный конец.
-
Автор:
mcneil - 6 лет назад
-
0
-
-
Логарифм (по основанию 4) это возрастающая функция (на всей своей области определения), поэтому для того, чтобы значение больше какого-то значения той же функции, необходимо, чтобы аргумент был больше см. вниз.
Ну и не забываем, про область допустимых значений из аргумента логарифма, ведь положительное число можно возвести только в положительное число.
Отметим интервалы и найдём пересечение.

-
Автор:
beetle71vm - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Допоможіть перекласти текст не перекладачом там багато помилок
Привіт, друзі! Мене звуть Ярина. Мені 16 років. Я не працюю, я вчуся. І я вчу німецьку мову. Я іноді ледача але старанно вивчаю граматику, виконую вcі вправи. Завдання не легкі, але цікаві. Я вчу слова і читаю вголос текст. У мене є німецько-український словник. Це подарунок моєї сестри. Я читаю словник і вивчаю слова. Я роблю це з великим задоволенням . У мене є друг який охоче допомагає мені. Він вже добре говорить німецькою.Його сестра живе у Німеччині.Як ви вивчаєте німецьку мову? Чи є у вас словник? Хто допомагає вам(euch)? Bеликий привіт! Ваша Яринка.-
Предмет:
Немецкий язык -
Автор:
moochiekemp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите, пожалуйста, задачу. Нужно решение.
Прямоугольный треугольник с катетами 11 см и 60 см вращают вокруг меньшего катета. Найдите поверхность полученного тела.-
Предмет:
Геометрия -
Автор:
adelynkirby - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
87.1Write sentences about Liz and Ben. Use than
87.2 Complete the sentences. Use than-
Предмет:
Английский язык -
Автор:
kyler113 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Повість минулих літ охоплює період
-
Предмет:
Українська література -
Автор:
codi4sfs - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years