Здравствуйте, помогите решить интеграл. Ответ должен получится: 2/3

Здравствуйте, помогите решить интеграл. Ответ должен получится: 2/3
- Предмет:
  Алгебра
- Автор:
  dottie
- 5 лет назад

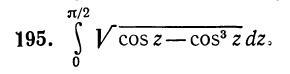
Ответы 6

Спасибо за очень хорошее и понятное объяснение! Вы лучший.
- Автор:
  patcheshouse
- 5 лет назад
- 0
В условии сказано, что нужно через замену решить. Сможете помочь?
- Автор:
  titan10
- 5 лет назад
- 0
Прошу прощения, что долго не отвечал. Сессия все-таки. Экзамены)) Интеграл попробую заменой решить, правда, ничего не могу обещать, так как интегральное исчисление было 2 года назад)))
- Автор:
  doran
- 5 лет назад
- 0
К сожалению, решение не могу теперь изменить. Но с заменой ещё проще оказалось. Корень от косинуса замени на t. Производная его в решение написана. С синусом ничего не делай, когда выразишь дифференциал, он сократится. Останетcя -2t* sqrt(cosx)*dt, корень этот меняешь ещё разок, и останется интеграл от -2t^2dt по пределам от 1 до 0 (это важно, но думаю, ты в состоянии посчитать новые пределы), взяв этот простой интеграл, убедишься, что ответ такой же: 2/3
- Автор:
  cindyjensen
- 5 лет назад
- 0
Да, все проверил, спасибо. Не знал какую замену подобрать.
- Автор:
  chandler
- 5 лет назад
- 0
Ответ:
Как ни странно, ответ здесь действительно 2/3
Объяснение:
Я надеюсь, z здесь никак не связано с комплексными числами. Решаем все это добро на множестве действительных чисел (мне несколько удобнее записывать через x, поэтому буду через х записывать. Думаю, переписать решение, заменив везде x на z, не проблема.)
$\int\limits^\frac{\pi }{2} _0 {\sqrt{cosx(1-cos^2x)} } \, dx =\int\limits^\frac{\pi }{2} _0 {\sqrt{cosx*sin^2x} } \, dx = \int\limits^\frac{\pi }{2} _0 |sinx|{\sqrt{cosx} } \, dx$
Теперь учтем, что пределы интегрирования предполагают, что в этом промежутке синус неотрицателен, а значит, его можно раскрыть со знаком "+".
$\int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \, dx$
Встает вопрос, что делать с этим интегралом. Попробуем интегрировать по частям. Для этого корень будем дифференцировать, а синус интегрировать. $\int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \, dx = -cosx\sqrt{cosx} - \int\limits^\frac{\pi }{2} _0 {\frac{sinxcosx}{2\sqrt{cosx} } } \, dx=-cosx\sqrt{cosx}-\frac{1}{2} \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \, dx$
Если не очень понятно про интегрирование по частям, почитай про него. Здесь важно, что: $(\sqrt{cosx})' = \frac{1}{2\sqrt{cosx} }*(-sinx)$ , и что $\int\limits^a_b {sinx} \, dx = -cosx$ (без подстановок и прочего) а потом лишь перемножения и вычитание.
Вернемся к интегралу. Занятно получилось, что в выражении спрятано некоторое уравнение относительно как раз нашего интеграла:
$\int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx = -cosx\sqrt{cosx} -\frac{1}{2} \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx$
Это вообще прекрасно, потому что мы уже фактически нашли наш интеграл:
$\frac{3}{2} \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx = -cosx\sqrt{cosx}; \int\limits^\frac{\pi }{2} _0 sinx{\sqrt{cosx} } \ dx = -\frac{2}{3}cosx\sqrt{cosx}$
Естественно, подразумевается, что значение справа вычисляется по двойной подстановке с теми пределами, которые у нас есть.
$-\frac{2}{3}(cos\frac{\pi }{2}\sqrt{cos\frac{\pi }{2} }-cos0\sqrt{cos0})=-\frac{2}{3}(0-1)=\frac{2}{3}$
Вот и получили наш ответ.
- Автор:
  cookie dough
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Здравствуйте, помогите решить интеграл. Ответ должен получится: 2/3

Ответы 6

Топ пользователей