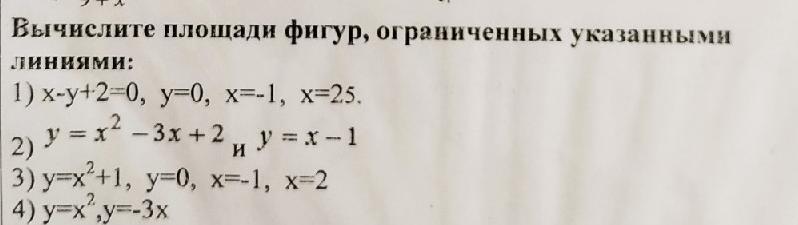Вычислить площади фигур, ограниченных указанными линиями

1) Для вычисления площади фигуры, ограниченной линиями x-y+2=0, y=0, x=-1, x=25, мы должны найти точки пересечения этих линий и использовать их для определения границ фигуры.

Из уравнения x-y+2=0, мы можем найти y:

y = x + 2.

Теперь мы можем найти точки пересечения линий:

1) При x = -1, y = -1 + 2 = 1. Точка пересечения: (-1, 1).

2) При x = 25, y = 25 + 2 = 27. Точка пересечения: (25, 27).

Таким образом, фигура ограничена линиями y=0, x=-1, x=25 и кривой y=x+2 между точками (-1, 1) и (25, 27). Для вычисления площади мы можем разделить эту фигуру на две части - треугольник и трапецию.

1) Площадь треугольника:

S1 = (1/2) base height = (1/2) (25 - (-1)) 1 = 13.

2) Площадь трапеции:

S2 = (1/2) (base1 + base2) height = (1/2) ((25 - (-1)) + (27 - 1)) (27 - 1) = 364.

Общая площадь фигуры:

S = S1 + S2 = 13 + 364 = 377.

Таким образом, площадь фигуры, ограниченной линиями x-y+2=0, y=0, x=-1, x=25, равна 377 единицам площади.

2) Для вычисления площади фигуры, ограниченной линиями y = x^2 - 3x + 2, y = x - 1, нам нужно найти точки пересечения этих двух кривых.

Для этого, приравняем выражения для y и решим квадратное уравнение:

x^2 - 3x + 2 = x - 1.

Это уравнение приводит к x^2 - 4x + 3 = 0, которое можно факторизовать как (x - 3)(x - 1) = 0.

Таким образом, у нас есть две точки пересечения: x = 1 и x = 3.

Подставим эти значения x в уравнения, чтобы найти соответствующие значения y:

При x = 1, y = 1^2 - 3(1) + 2 = 0.

При x = 3, y = 3^2 - 3(3) + 2 = 2.

Таким образом, у нас есть две точки пересечения: (1, 0) и (3, 2).

Фигура ограничена линиями y = x^2 - 3x + 2, y = x - 1 и осью x. Мы можем вычислить площадь этой фигуры, используя метод интегрирования.

3) Для вычисления площади фигуры, ограниченной линиями y = x + 1, y = 0, x = -1, x = 2, мы можем использовать метод интегрирования.

Линии y = x + 1 и y = 0 пересекаются при x = -1 и x = 2.

То есть, фигура ограничена вертикальными линиями x = -1 и x = 2, горизонтальной линией y = 0 и кривой y = x + 1 между этими точками.

Площадь этой фигуры можно вычислить, интегрируя функцию y = x + 1 от x = -1 до x = 2.

4) Для вычисления площади фигуры, ограниченной линиями y = x^2 и y = -3x, мы должны найти точки пересечения этих двух кривых.

Для этого, приравняем выражения для y и решим уравнение:

x^2 = -3x.

Это уравнение приводит к x^2 + 3x = 0, которое можно факторизовать как x(x + 3) = 0.

Таким образом, у нас есть две точки пересечения: x = 0 и x = -3.

Подставим эти значения x в уравнения, чтобы найти соответствующие значения y:

При x = 0, y = 0^2 = 0.

При x = -3, y = (-3)^2 = 9.

Таким образом, у нас есть две точки пересечения: (0, 0) и (-3, 9).

Фигура ограничена линиями y = x^2 и y = -3x. Мы можем вычислить площадь этой фигуры, используя метод интегрирования...