Дослідіть функцію на парність f(x)= (xsinx) / (1-cosx) потрібне пояснення, дякую Не крадіть бали, будь ласка!

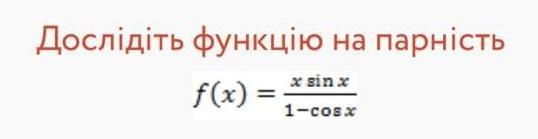
Ответ: Функцію f(x) = (x * sin(x)) / (1 - cos(x)) можна дослідити на її парність, подивившись на поведінку функції, коли x замінено на -x. Парність означає, чи є функція парною, непарною чи ні.

Парна функція — це така, для якої f(-x) = f(x). Непарна функція - це така, для якої f(-x) = -f(x). Якщо функція не є ні парною, ні непарною, її називають змішаною.

Щоб визначити парність f(x), ми можемо замінити x на -x:

f(-x) = (x * sin(-x)) / (1 - cos(-x))

Використовуючи тригонометричну тотожність sin(-x) = -sin(x) і cos(-x) = cos(x), ми можемо спростити:

f(-x) = (-x * -sin(x)) / (1 - cos(x))

f(-x) = (x * sin(x)) / (1 - cos(x))

Оскільки f(-x) = f(x), можна зробити висновок, що функція f(x) парна.