умоляю помогите решить полностью тождество пожалуйста полностьюдам 60 баллов и сделаю лучший ответ ​

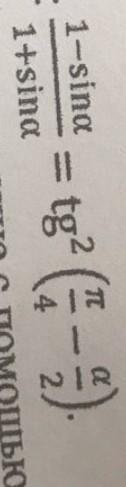
Ответ:

Объяснение:

Преобразуем правую часть .

tg²(π/4-α/2)= sin²(π/4-α/2) /(cos²(π/4-α/2))

sin²(π/4-α/2)=(sin(π/4)·cos(α/2) - cos(π/4)*sin(α/2))² =

(√2/2·cos(α/2) -√2/2·sin(α/2))² =0.5((cos(α/2) -sin(α/2))² =

=0.5(cos²(α/2) -2·sin(α/2)·cos(α/2)+ sin²(α/2))=0.5 (1-2·sin(α/2)·cos(α/2))=

=0.5(1-sinα)

cos²(π/4-α/2)=(cos(π/4)·cos(α/2) + sin(π/4)*sin(α/2))² =

(√2/2·cos(α/2) +√2/2·sin(α/2))² =0.5((cos(α/2) +sin(α/2))² =

=0.5(cos²(α/2) +2·sin(α/2)·cos(α/2)+ sin²(α/2))=0.5 (1+2·sin(α/2)·cos(α/2))=

=0.5(1+sinα)

=> правая часть = 0.5(1-sinα)/(0.5(1+sinα))=(1-sinα)/(1+sinα)