70 балів!! За спам баню!! Допоможіть зробити 3 номер.​

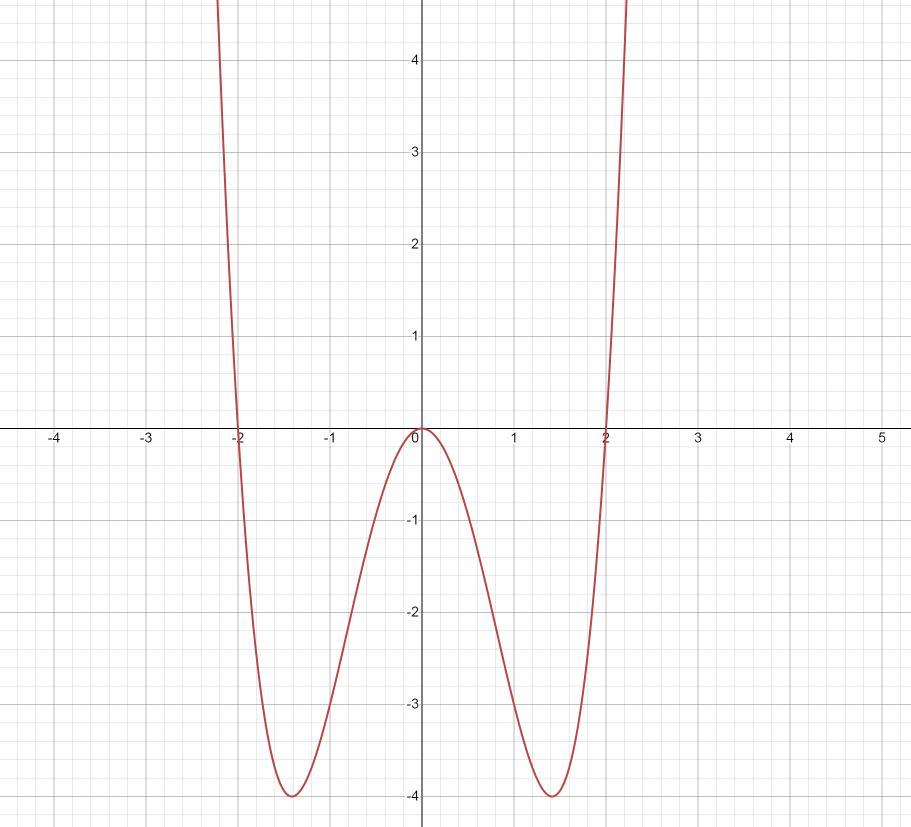
Для дослідження функції y = x^4 - 4x^2 спочатку знайдемо її похідні:

y' = 4x^3 - 8x

y'' = 12x^2 - 8

Тепер проаналізуємо властивості функції:

Область визначення: функція визначена для будь-якого значення x.

Знак функції y: розкладаємо функцію на множники:

y = x^4 - 4x^2 = x^2(x^2 - 4) = x^2(x+2)(x-2)

Отже, знак функції залежить від знаку множників. Для x<0 функція y<0, для 0<x< -2 функція y>0, для -2<x<2 функція y<0, і для x>2 функція y>0. Звідси можна побачити, що функція має мінімум у точці x=-2 і максимум у точці x=2.

Точки перетину з осями координат:

y(0) = 0

y(±2) = 0

Знак похідної:

y' = 4x^3 - 8x = 4x(x^2 - 2)

Якщо x < -√2 або -√2 < x < 0, то y' < 0; якщо -√2 < x < √2, то y' > 0; і якщо x > √2, то y' < 0.

Отже, функція має максимум у точці x=-√2 та мінімум у точці x=√2.

Знак другої похідної:

y'' = 12x^2 - 8

Якщо x < -√(2/3) або x > √(2/3), то y'' > 0; якщо -√(2/3) < x < √(2/3), то y'' < 0.

Отже, точки x=-√(2/3) та x=√(2/3) є точками перегину другої похідної, і вони відповідають точкам зміни знаку другої похідної.