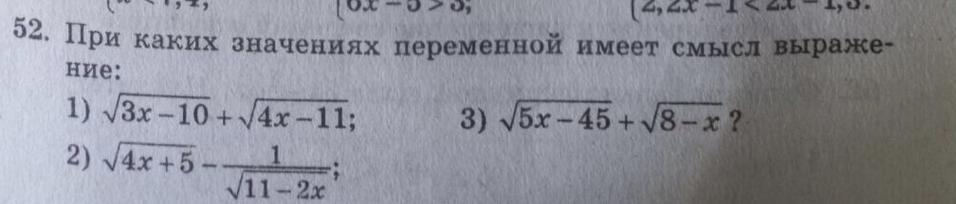Ответы 1
-
Ответ:
Дробь имеет смысл при тех значениях переменной, при которых знаменатель дроби не равен 0 . Подкоренное выражение корня чётной степени должно быть неотрицательным .
\bf 1)\ \ \sqrt{3x-10}+\sqrt{4x-11}\ \ \ \Rightarrow \ \ \ \left\{\begin{array}{l}\bf 3x-10\geq 0\ ,\\\bf 4x-11\geq 0\ ,\end{array}\right\ \ \left\{\begin{array}{l}\bf x\geq \dfrac{10}{3}\ ,\\\bf \ \ x\geq \dfrac{11}{4}\ ,\end{array}\right\\\\\\\left\{\begin{array}{l}\bf x\geq 3\dfrac{1}{3}\ ,\\\bf \ \ x\geq 2\dfrac{3}{4}\ ,\end{array}\right\ \ \ \Rightarrow \ \ \ x\geq 3\dfrac{1}{3}
\bf 2)\ \ \sqrt{4x+5}-\dfrac{1}{\sqrt{11-2x}}\ \ \ \Rightarrow \ \ \ \left\{\begin{array}{l}\bf 4x+5\geq 0\ ,\\\bf 11-2x\geq 0\ ,\end{array}\right\ \ \left\{\begin{array}{l}\bf \ x\geq -\dfrac{5}{4}\ ,\\\bf x\leq \dfrac{11}{2}\ ,\end{array}\right\\\\\\\left\{\begin{array}{l}\bf x\geq -1,25\ ,\\\bf x\leq 5,5\ ,\end{array}\right\ \ \Rightarrow \ \ \ -1,25\leq x\leq 5,5
\bf 3)\ \ \sqrt{5x-45}+\sqrt{8-x}\ \ \ \Rightarrow \ \ \ \left\{\begin{array}{l}\bf 5x-45\geq 0\ ,\\\bf 8-x\geq 0\ ,\end{array}\right\ \ \left\{\begin{array}{l}\bf 5x\geq 45\ ,\\\bf -x\geq -8\ ,\end{array}\right\\\\\\\left\{\begin{array}{l}\bf x\geq 9\ ,\\\bf x\leq 8\ ,\end{array}\right\ \ \Rightarrow \ \ \ x\in \varnothing

-
Автор:
leocadialens - 2 года назад
-
2
-
-
Добавить свой ответ
-
Помогите пожалуйста. Учу комбинаторику но не могу понять одну вещь. A15⁵ = 15•(15-1)(15-2)(15-3(15-4). Хо ел бы спросить нужно ли дописывать (15-5+1) ведь по сути это одно и тоже с (15-4) или же нужно писать только (15-5+1)?
-
Предмет:
Математика -
Автор:
víctor65 - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
ABCD - просторовий чотирикутник (вершини не належать одній площині), точки F, G, K, L - середини відрізків AB, BD, DC і АС відповідно. Знайдіть периметр чотирикутника FGKL, якщо
ВС = 11,7 см, AD = 13,5 см
-
Предмет:
Математика -
Автор:
william98 - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Помогите решить две задачи. 1.Периметр трикутника дорівнює 84 см, Бісектриса його кута ділить сторону на відрізки 10,5см і 17,5см.Знайти сторони тринутника 2. Бісектриса прямого кута прямокутного трикутника ділить його сторону на відрізки 60см і 45. Знайти периметр трикутника
-
Впр. 2. Перекладіть англійською мовою, вживаючи дієсло- вa y Present, Past ra Future Simple Passive. 1. Менi розказали Мені розказують Менi розкажуть 2. Йому показали Йому показують Йому покажуть 3. Їй дали Їй дають Iй дадуть 4. Менi допомогли Мені допомагають Мені допоможуть 5. Його помітили Його помічають Його помітять 6. Нас запросили Нас запрошують Нас запросять 7. Їм дозволили Їм дозволяють ÎM дозволять 8. Їй Їй радять Їй порадять Його чують Його Почують Менi вiрять Менi повірять Їх впізнають Їх впізнають Його згадують Його згадають порадили 9. Його почули 10. Мені повірили 11. Їх впізнали 12. Його згадали
-
Предмет:
Английский язык -
Автор:
núñez76 - 2 года назад
-
Ответов:
1 -
Смотреть
-