-
Докажите, что при любом натуральном n ∈ ℕ выполняется: (1/(n+1) + 1/(n+2) + ... + 1/(2n+2) ) > 13/24
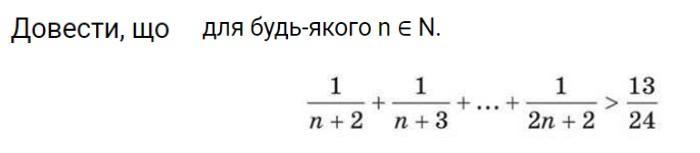
Ответы 1
-
Відповідь:Для доведення нерівності, спростимо ліву частину:
(1/(n+1) + 1/(n+2) + ... + 1/(2n+2))
Знайдемо спільний знаменник для усіх дробів, це буде (n + 1) * (n + 2):
= (1 * (n+2) + 1 * (n+1) + ... + 1 * 1) / ((n+1) * (n+2))
Тепер обчислимо чисельник:
= ((n+2) + (n+1) + ... + 1) / ((n+1) * (n+2))
Це є сумою арифметичної прогресії від 1 до (n + 2) з різницею 1:
= ((n + 2) * (n + 3)) / 2 / ((n+1) * (n+2))
Зараз спростимо вираз, поділивши чисельник і знаменник на (n + 2):
= ((n + 3) / 2) / (n + 1)
Залишаємо лише цей вираз:
= (n + 3) / (2 * (n + 1))
Тепер можемо перевірити нерівність:
(n + 3) / (2 * (n + 1)) > 13/24
Перемножимо обидві сторони на 2 * (n + 1), щоб позбутися від знаменника:
(n + 3) > (13/24) * (2 * (n + 1))
Розкриємо дужки:
n + 3 > (13/12) * (n + 1)
Розкриємо дужки в правій частині нерівності:
n + 3 > (13/12) * n + (13/12)
Віднімемо (13/12) * n з обох сторін:
3 > (13/12) + (13/12) * n - (13/12) * n
Залишаємо лише числа:
3 > 13/12
Ця нерівність завжди вірна, оскільки 3 більше, ніж 13/12.
Отже, ми довели, що для будь-якого натурального n ∈ ℕ нерівність:
(1/(n+1) + 1/(n+2) + ... + 1/(2n+2)) > 13/24
Пояснення:
-
Автор:
concepciónmarshall - 2 года назад
-
5
-
-
Добавить свой ответ
- Помогите пожалуйста сравнить цены.
- Какова специфика атомной электростанции?
-
Дати розгорнуті відповіді на питання ( 2 -4 ) речення
Питання.
1.Як ви розумієте термін - суспільно - побутові пісні?
2.Які пісні народ називає козацькими?
3. Що таке пафос? Пояснити прикладом козацької пісні?
4. Дібрати до слова "гомін" синоніми, пояснити значення.
5. Яка соціально - побутова пісня вам найбільше сподобалася? Чим?
6. У чому полягає особливість коломийок?
Тількі будль ласка, не з інтернету, а своїми словами(хочаб 2-3 питання)
-
Предмет:
Литература -
Автор:
knight - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Задача по физике про парашютиста.
-
Предмет:
Физика -
Автор:
antonpotts - 2 года назад
-
Ответов:
4 -
Смотреть
-
