СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА ДАЮ 50 БАЛЛОВ Определить, сколько целых решений имеет неравенство на интервале (0; 2п) \sin(2x + \frac{\pi}{3} ) \leqslant \frac{1}{2} ​

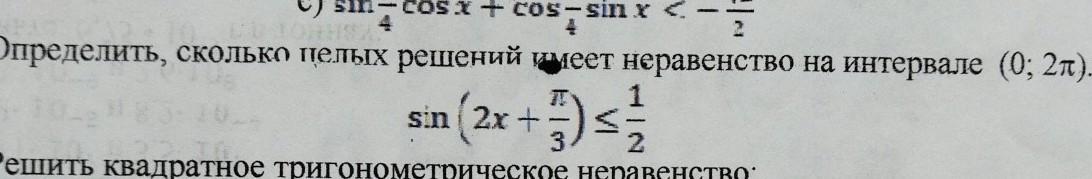
Ответ:

Для розв'язання нерівності спочатку знайдемо значення аргументу (2x + π/3), при якому sin(2x + π/3) = 1/2.

Так як sin(π/6) = 1/2, то отримаємо:

2x + π/3 = π/6 + 2kπ, де k - ціле число.

Розв'яжемо рівняння відносно x:

2x = -π/6 + 2kπ - π/3

x = -π/12 + kπ - π/6

x = -π/12 - π/6 + kπ

x = -π/4 + kπ

Тепер ми можемо визначити інтервали, на яких нерівність виконується. Для цього розглянемо інтервали між точками перетину графіків sin(2x + π/3) і 1/2, а також між точками перетину графіків sin(2x + π/3) і -1/2.

Отримаємо такі інтервали:

(-∞, -π/4), (-π/4, π/4), (π/4, 3π/4), (3π/4, 5π/4), (5π/4, ∞)

Тепер перевіримо значення sin(2x + π/3) на кожному з цих інтервалів. Якщо sin(2x + π/3) знаходиться в межах від -1/2 до 1/2, то нерівність виконується.

Отже, нерівність має цілком розв'язків на інтервалах (-π/4, π/4) та (3π/4, 5π/4).