-
3. В геометрической прогрессин (b) прогрессии. известно b1 = 5, q = -2. Запишите первые пять членов
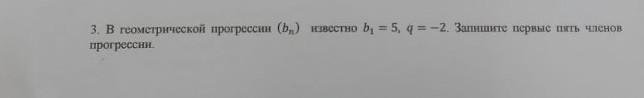
-
Предмет:
Алгебра -
Автор:
ethanwilliams - 2 года назад
-
Ответы 1
-
Ответ:
Объяснение:
Для нахождения первых пяти членов геометрической прогрессии нужно использовать формулу:
bn = b1 * q^(n-1),
где:
bn - n-й член прогрессии,
b1 - первый член прогрессии,
q - знаменатель прогрессии,
n - номер члена прогрессии.
Исходя из условия, где b1 = 5 и q = -2, мы можем подставить эти значения в формулу и вычислить первые пять членов:
b1 = 5
b2 = b1 * q = 5 * (-2) = -10
b3 = b1 * q^2 = 5 * (-2)^2 = -20
b4 = b1 * q^3 = 5 * (-2)^3 = -40
b5 = b1 * q^4 = 5 * (-2)^4 = -80
Таким образом, первые пять членов геометрической прогрессии с b1 = 5 и q = -2 будут:
5, -10, -20, -40, -80.
-
Автор:
darrenznkv - 2 года назад
-
2
-
-
Добавить свой ответ
Еще вопросы
- Мідний дріт масою 44,5 кг має опір 3.4 Ом. Визначте його довжину. Питомий опір міді 1,7*10⁻⁸Ом*м, густина міді 8900 кг/м³.
-
Короткий пересказ Гоголя старосветские помещики
-
Предмет:
Литература -
Автор:
anascott - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
Образуйте относительные прилагательные с помощью суффиксов объясните почему в них пишется Н или Н Н свобода свободный лес прочесть грусть книга
-
Предмет:
Литература -
Автор:
smokey - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Вопрос по литературе
-
Предмет:
Литература -
Автор:
brunohunt - 2 года назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
