-
22.20. Докажите, что при всех допустимых значениях а является постоянной величиной значение выражения: (tga + ctga)2 - (tga 1 cos² a . sin2 a 2) cos'a + sina + 3cos²a . sin²a. 1) (tga - ctga)2 ctg²a - tg² a ;
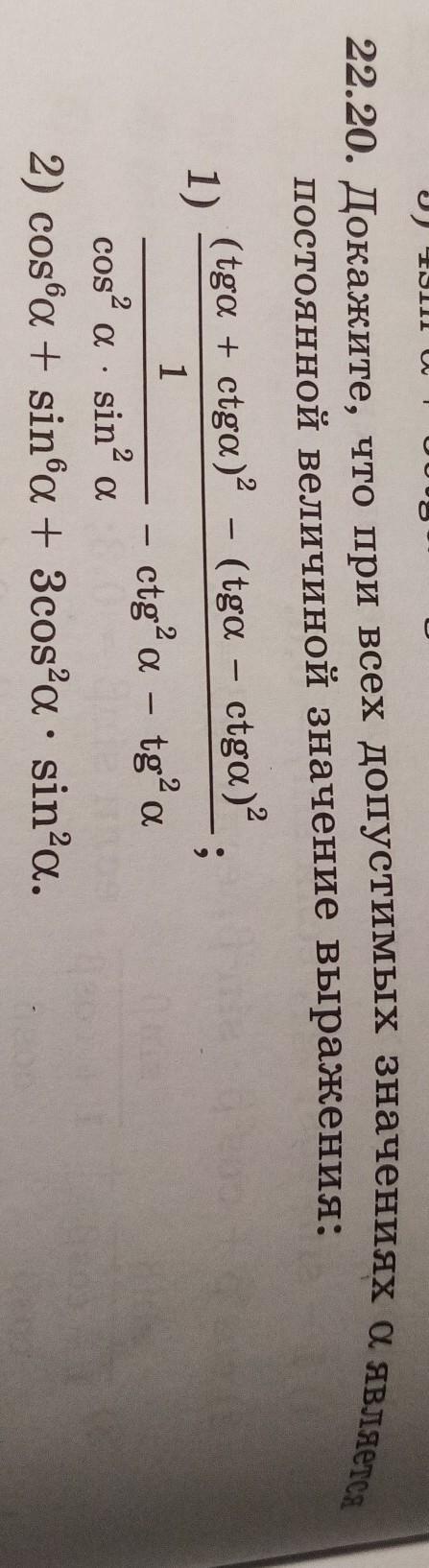
-
Предмет:
Алгебра -
Автор:
charlespeterson - 2 года назад
-
Ответы 1
-
Чтобы доказать, что данное выражение постоянно при всех допустимых значениях \(a\), давайте рассмотрим выражение и упростим его:\[ (tg a + ctg a)^2 - (tg a - ctg a)^2 \]Воспользуемся разностью квадратов:\[ (tg^2 a + 2tg a \cdot ctg a + ctg^2 a) - (tg^2 a - 2tg a \cdot ctg a + ctg^2 a) \]Сократим подобные члены:\[ 4tg a \cdot ctg a \]Теперь у нас есть упрощенное выражение. Давайте сравним его с второй частью выражения:\[ ctg^2 a - tg^2 a \]Также воспользуемся тригонометрическими тождествами:\[ ctg^2 a - tg^2 a = \frac{cos^2 a}{sin^2 a} - \frac{sin^2 a}{cos^2 a} \]Общий знаменатель:\[ \frac{cos^4 a - sin^4 a}{sin^2 a \cdot cos^2 a} \]Тождество \(cos^4 a - sin^4 a = (cos^2 a - sin^2 a) \cdot (cos^2 a + sin^2 a)\) позволяет упростить выражение:\[ \frac{(cos^2 a - sin^2 a) \cdot (cos^2 a + sin^2 a)}{sin^2 a \cdot cos^2 a} \]Так как \(cos^2 a + sin^2 a = 1\), получаем:\[ \frac{cos^2 a - sin^2 a}{sin^2 a \cdot cos^2 a} \]Теперь у нас есть \(ctg^2 a - tg^2 a\) в терминах тригонометрических функций. Подставим его в начальное выражение:\[ 4tg a \cdot ctg a = ctg^2 a - tg^2 a \]Таким образом, доказано, что заданное выражение постоянно при всех допустимых значениях \(a\).
-
Автор:
dharma55dg - 2 года назад
-
5
-
-
Добавить свой ответ
Еще вопросы
-
5 розділових запитань (чи не так?) на англійській мові!!!!
СРОЧНО,дам багато балів!!!!
-
Предмет:
Английский язык -
Автор:
sydneyturner - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Очистка озера, природа!
-
Предмет:
Обществознание -
Автор:
ringowoodward - 2 года назад
-
Ответов:
3 -
Смотреть
-
-
Влияние физического воспитания и черного труда на здоровье. конспект пж
-
Предмет:
Биология -
Автор:
milaguerra - 2 года назад
-
Ответов:
1 -
Смотреть
-
- 48y²+8y-1=0решите через дискриминант
How much to ban the user?
1 hour
1 day
100 years
