-
При каких значениях р вершина параболы y = x^2+4x+p pacположена на расстоянии, равном 4 от начала координат?
-
Предмет:
Алгебра -
Автор:
fitzpatrick - 2 года назад
-
Ответы 1
-
Ответ:
p = 4
Объяснение:
Чтобы найти значения ( p ), при которых вершина параболы ( y = x^2 + 4x + p ) находится на расстоянии, равном 4 от начала координат, нужно использовать формулу для координат вершины параболы ( (h, k) ):
h=-b/2a
где (а=1) (b=4) (c=p)
Подставляя значения ( h ) и ( k ) и решая уравнение относительно ( p ), получаем:
(фото 1)
Теперь нужно решить это квадратное уравнение относительно ( p ).
Из уравнения ( h^2 + 4h + p = 0 ) видно, что вершина параболы находится на расстоянии 4 от начала координат, когда дискриминант этого квадратного уравнения равен нулю.Дискриминант ( D ) квадратного уравнения ( ax^2 + bx + c = 0 ) равен ( D = b^2 - 4ac ).В данном случае ( a = 1 ), ( b = 4 ), ( c = p ). Подставим эти значения в формулу для дискриминанта:
D = 4² - 4 * 1 * p
Теперь, чтобы найти значения ( p ), при которых вершина параболы ( y = x^2 + 4x + p ) находится на расстоянии 4 от начала координат, нужно приравнять дискриминант к нулю и решить полученное уравнение:
[ D = 16 - 4p = 0 ] [ 16 = 4p ] [ p = 4 ]
Таким образом, вершина параболы ( y = x^2 + 4x + p ) находится на расстоянии 4 от начала координат при ( p = 4 ).
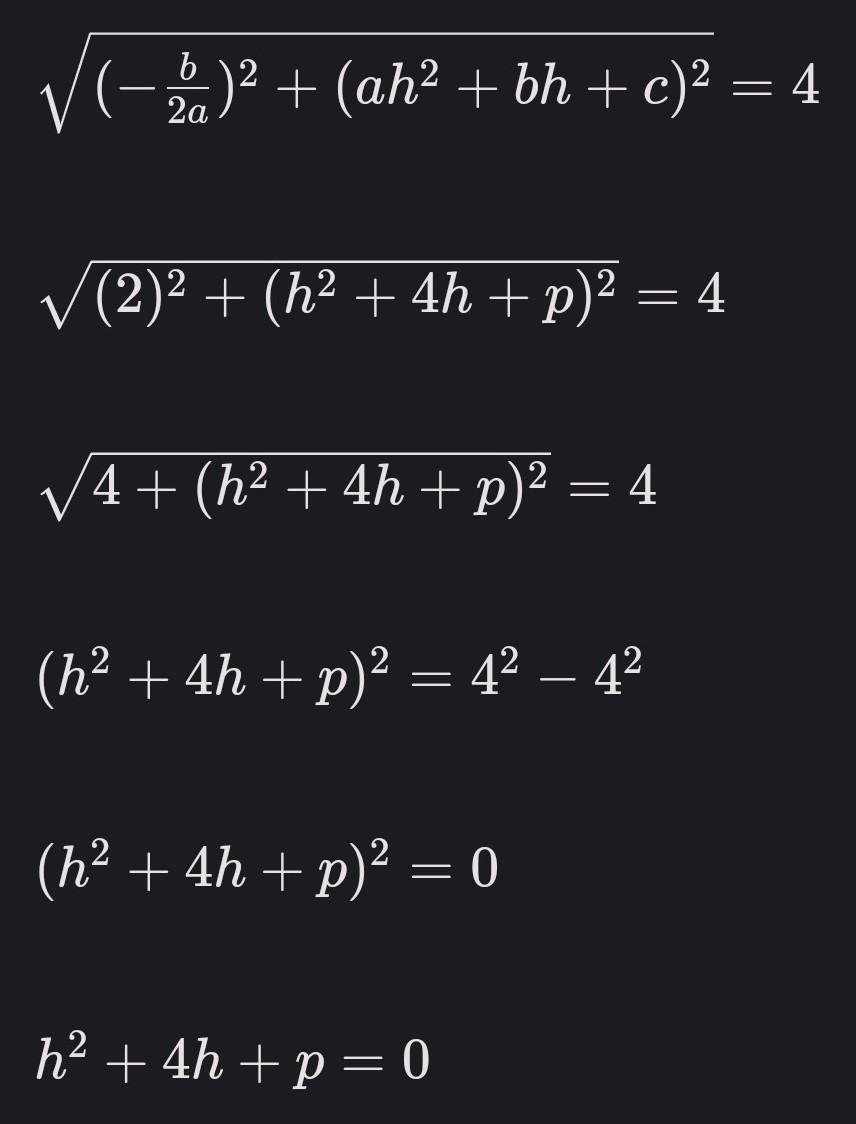
-
Автор:
baileygwjp - 2 года назад
-
3
-
-
Добавить свой ответ
-
Помогите срочно нужно 4 предложения с Деепричастным оборотом из рассказа тоска Чехов
-
Предмет:
Русский язык -
Автор:
peck - 2 года назад
-
Ответов:
3 -
Смотреть
-
- виберіть з переоіку етапи ембіогенезу рослин а утворення із зиготи зародкової твірної тканини б утворення зародкових органів корінця і пагінця в формування насінини г формування кореня ТІЛЬКИ БУКВУ БУДЬ-ЛАСКА!
-
Берілген сөздер мен сөз тіркестерін қатыстыра отырып, сөйлем құрастырыңдар. Ақыл-ой,тәрбие,жетілдіру, білім жолында, болашаққа бағдар, әдеби , көркем шығарма,жүктелген міндет,шынайы білімді адам,жас ұрпақ, болашақ тірегі,алға ұмтылу, мақсатқа жету, жан-жақты білім алу, сөз әдебі, мәдениет,өркениет.
-
Предмет:
Қазақ тiлi -
Автор:
niki95 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Что такое безочлен?
-
Предмет:
Русский язык -
Автор:
giancarlo - 2 года назад
-
Ответов:
3 -
Смотреть
-
