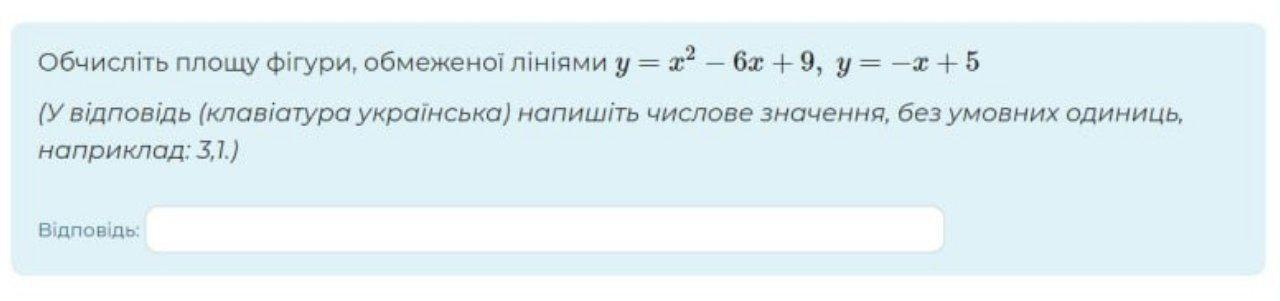
Обчисліть площу фігури, обмеженої лініями y = x^2 - 6x + 9 y = -x + 5

Ответ:

Щоб обчислити площу фігури, обмеженоє лініями y = x^2 - 6x + 9 та y = -x + 5, спочатку потрібно знайти точки їх перетину. Далі, обчислити площу обмеженої фігури, використавши інтеграл.

Знайдемо точки перетину: x^2 - 6x + 9 = -x + 5 x^2 - 5x + 4 = 0 (x - 4)(x - 1) = 0 x1 = 4 x2 = 1

Таким чином, точки перетину цих двох функцій - (4, 1) та (1, 4).

Тепер, обчислимо площу фігури, обмеженоє цими лініями: ∫[1,4] ((x^2 - 6x + 9) - (-x + 5)) dx = ∫[1,4] (x^2 - 6x + 9 + x - 5) dx = ∫[1,4] (x^2 - 5x + 4) dx = [((x^3)/3) - (5x^2)/2 + 4x] [1,4] = ((4^3)/3 - (54^2)/2 + 44) - ((1^3)/3 - (51^2)/2 + 41) = (64/3 - 40/2 + 16) - (1/3 - 5/2 + 4) = (64/3 - 20 + 16) - (1/3 - 5/2 + 4) = 64/3 - 4 - 1/3 + 5/2 = 64/3 - 12/3 - 1/3 + 15/6 = 51/6 = 8.5

Таким чином, площа фігури обмеженоє лініями y = x^2 - 6x + 9 та y = -x + 5 дорівнює 8.5 квадратними одиницями.